A brief primer on Variational Inference

Bayesian inference using Markov chain Monte Carlo methods can be notoriously slow. In this blog post, we reframe Bayesian inference as an optimization problem using variational inference, markedly speeding up computation. We derive the variational objective function, implement coordinate ascent mean-field variational inference for a simple linear regression example in R, and compare our results to results obtained via variational and exact inference using Stan. Sounds like word salad? Then let’s start unpacking!

Preliminaries

Bayes’ rule states that

\[\underbrace{p(\mathbf{z} \mid \mathbf{x})}_{\text{Posterior}} = \underbrace{p(\mathbf{z})}_{\text{Prior}} \times \frac{\overbrace{p(\mathbf{x} \mid \mathbf{z})}^{\text{Likelihood}}}{\underbrace{\int p(\mathbf{x} \mid \mathbf{z}) \, p(\mathbf{z}) \, \mathrm{d}\mathbf{z}}_{\text{Marginal Likelihood}}} \enspace ,\]

where $\mathbf{z}$ denotes latent parameters we want to infer and $\mathbf{x}$ denotes data.¹ Bayes’ rule is, in general, difficult to apply because it requires dealing with a potentially high-dimensional integral — the marginal likelihood. Optimization, which involves taking derivatives instead of integrating, is much easier and generally faster than the latter, and so our goal will be to reframe this integration problem as one of optimization.

Variational objective

We want to get at the posterior distribution, but instead of sampling we simply try to find a density $q^\star(\mathbf{z})$ from a family of densities $\mathrm{Q}$ that best approximates the posterior distribution:

\[q^\star(\mathbf{z}) = \underbrace{\text{argmin}}_{q(\mathbf{z}) \in \mathrm{Q}} \text{ KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z} \mid \mathbf{x}) \right) \enspace ,\]

where $\text{KL}(. \lvert \lvert.)$ denotes the Kullback-Leibler divergence:

\[\text{KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z} \mid \mathbf{x}) \right) = \int q(\mathbf{z}) \, \text{log } \frac{q(\mathbf{z})}{p(\mathbf{z} \mid \mathbf{x})} \mathrm{d}\mathbf{z} \enspace .\]

We cannot compute this Kullback-Leibler divergence because it still depends on the nasty integral $p(\mathbf{x}) = \int p(\mathbf{x} \mid \mathbf{z}) \, p(\mathbf{z}) \, \mathrm{d}\mathbf{z}$. To see this dependency, observe that:

\[\begin{aligned} \text{KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z} \mid \mathbf{x}) \right) &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } \frac{q(\mathbf{z})}{p(\mathbf{z} \mid \mathbf{x})}\right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z} \mid \mathbf{x})\right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } \frac{p(\mathbf{z}, \mathbf{x})}{p(\mathbf{x})}\right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] + \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{x})\right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] + \int q(\mathbf{z}) \, \text{log } p(\mathbf{x}) \, \mathrm{d}\mathbf{z} \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] + \underbrace{\text{log } p(\mathbf{x})}_{\text{Nemesis}} \enspace , \end{aligned}\]

where we have expanded the expectation to more clearly behold our nemesis. In doing so, we have seen that $\text{log } p(\mathbf{x})$ is actually a constant with respect to $q(\mathbf{z})$; this means that we can ignore it in our optimization problem. Moreover, minimizing a quantity means maximizing its negative, and so we maximize the following quantity:

\[\begin{aligned} \text{ELBO}(q) &= -\left(\text{KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z} \mid \mathbf{x}) \right) - \text{log } p(\mathbf{x}) \right) \\[.5em] &= -\left(\mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] + \underbrace{\text{log } p(\mathbf{x}) - \text{log } p(\mathbf{x})}_{\text{Nemesis perishes}}\right) \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] \enspace . \end{aligned}\]

We can expand the joint probability to get more insight into this equation:

\[\begin{aligned} \text{ELBO}(q) &= \underbrace{\mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{x} \mid \mathbf{z})\right] + \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z})\right]}_{\mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right]} - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{x} \mid \mathbf{z})\right] + \mathbb{E}_{q(\mathbf{z})}\left[\text{log } \frac{p(\mathbf{z})}{q(\mathbf{z})}\right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{x} \mid \mathbf{z})\right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } \frac{q(\mathbf{z})}{p(\mathbf{z})}\right] \\[.5em] &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{x} \mid \mathbf{z})\right] - \text{KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z})\right) \enspace . \end{aligned}\]

This is cool. It says that maximizing the ELBO finds an approximate distribution $q(\mathbf{z})$ for latent quantities $\mathbf{z}$ that allows the data to be predicted well, i.e., leads to a high expected log likelihood, but that a penalty is incurred if $q(\mathbf{z})$ strays far away from the prior $p(\mathbf{z})$. This mirrors the usual balance in Bayesian inference between likelihood and prior (Blei, Kucukelbier, & McAuliffe, 2017).

ELBO stands for evidence lower bound. The marginal likelihood is sometimes called evidence, and we see that ELBO is indeed a lower bound for the evidence:

\[\begin{aligned} \text{ELBO}(q) &= -\left(\text{KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z} \mid \mathbf{x}) \right) - \text{log } p(\mathbf{x})\right) \\[.5em] \text{log } p(\mathbf{x}) &= \text{ELBO}(q) + \text{KL}\left(q(\mathbf{z}) \, \lvert\lvert \, p(\mathbf{z} \mid \mathbf{x}) \right) \\[.5em] \text{log } p(\mathbf{x}) &\geq \text{ELBO}(q) \enspace , \end{aligned}\]

since the Kullback-Leibler divergence is non-negative. Heuristically, one might then use the ELBO as a way to select between models. For more on predictive model selection, see this and this blog post.

Why variational?

Our optimization problem is about finding $q^\star(\mathbf{z})$ that best approximates the posterior distribution. This is in contrast to more familiar optimization problems such as maximum likelihood estimation where one wants to find, for example, the single best value that maximizes the log likelihood. For such a problem, one can use standard calculus (see for example this blog post). In our setting, we do not want to find a single best value but rather a single best function. To do this, we can use variational calculus from which variational inference derives its name (Bishop, 2006, p. 462).

A function takes an input value and returns an output value. We can define a functional which takes a whole function and returns an output value. The entropy of a probability distribution is a widely used functional:

\[\text{H}[p] = \int p(x) \, \text{log } p(x) \mathrm{d} x \enspace ,\]

which takes as input the probability distribution $p(x)$ and returns a single value, its entropy. In variational inference, we want to find the function that minimizes the ELBO, which is a functional.

In order to make this optimization problem more manageable, we need to constrain the functions in some way. One could, for example, assume that $q(\mathbf{z})$ is a Gaussian distribution with parameter vector $\omega$. The ELBO then becomes a function of $\omega$, and we employ standard optimization methods to solve this problem. Instead of restricting the parametric form of the variational distribution $q(\mathbf{z})$, in the next section we use an independence assumption to manage the inference problem.

Mean-field variational family

A frequently used approximation is to assume that the latent variables $z_j$ for $j = \{1, \ldots, m\}$ are mutually independent, each governed by their own variational density:

\[q(\mathbf{z}) = \prod_{j=1}^m q_j(z_j) \enspace .\]

Note that this mean-field variational family cannot model correlations in the posterior distribution; by construction, the latent parameters are mutually independent. Observe that we do not make any parametric assumption about the individual $q_j(z_j)$. Instead, their parametric form is derived for every particular inference problem.

We start from our definition of the ELBO and apply the mean-field assumption:

\[\begin{aligned} \text{ELBO}(q) &= \mathbb{E}_{q(\mathbf{z})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] - \mathbb{E}_{q(\mathbf{z})}\left[\text{log } q(\mathbf{z}) \right] \\[.5em] &= \int \prod_{i=1}^m q_i(z_i) \, \text{log } p(\mathbf{z}, \mathbf{x}) \, \mathrm{d}\mathbf{z} - \int \prod_{i=1}^m q_i(z_i) \, \text{log}\prod_{i=1}^m q_i(z_i) \, \mathrm{d}\mathbf{z}\enspace . \end{aligned}\]

In the following, we optimize the ELBO with respect to a single variational density $q_j(z_j)$ and assume that all others are fixed:

\[\begin{aligned} \text{ELBO}(q_j) &= \int \prod_{i=1}^m q_i(z_i) \, \text{log } p(\mathbf{z}, \mathbf{x}) \, \mathrm{d}\mathbf{z} - \int \prod_{i=1}^m q_i(z_i) \, \text{log}\prod_{i=1}^m q_i(z_i) \, \mathrm{d}\mathbf{z} \\[.5em] &= \int \prod_{i=1}^m q_i(z_i) \, \text{log } p(\mathbf{z}, \mathbf{x}) \, \mathrm{d}\mathbf{z} - \int q_j(z_j) \, \text{log } q_j(z_j) \, \mathrm{d}z_j - \underbrace{\int \prod_{i\neq j}^m q_i(z_i) \, \text{log} \prod_{i\neq j}^m q_i(z_i) \, \mathrm{d}\mathbf{z}_{-j}}_{\text{Constant with respect to } q_j(z_j)} \\[.5em] &\propto \int \prod_{i=1}^m q_i(z_i) \, \text{log } p(\mathbf{z}, \mathbf{x}) \, \mathrm{d}\mathbf{z} - \int q_j(z_j) \, \text{log } q_j(z_j) \, \mathrm{d}z_j \\[.5em] &= \int q_j(z_j) \left(\int \prod_{i\neq j}^m q_i(z_i) \, \text{log } p(\mathbf{z}, \mathbf{x}) \, \mathrm{d}\mathbf{z}_{-j}\right)\mathrm{d}z_j - \int q_j(z_j) \, \text{log } q_j(z_j) \, \mathrm{d}z_j \\[.5em] &= \int q_j(z_j) \, \mathbb{E}_{q(\mathbf{z}_{-j})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right]\mathrm{d}z_j - \int q_j(z_j) \, \text{log } q_j(z_j) \, \mathrm{d}z_j \enspace . \end{aligned}\]

One could use variational calculus to derive the optimal variational density $q_j^\star(z_j)$; instead, we follow Bishop (2006, p. 465) and define the distribution

\[\text{log } \tilde{p}{(\mathbf{x}, z_j)} = \mathbb{E}_{q(\mathbf{z}_{-j})}\left[\text{log } p(\mathbf{z}, \mathbf{x})\right] - \mathcal{Z} \enspace ,\]

where we need to make sure that it integrates to one by subtracting the (log) normalizing constant $\mathcal{Z}$. With this in mind, observe that:

\[\begin{aligned} \text{ELBO}(q_j) &\propto \int q_j(z_j) \, \text{log } \tilde{p}{(\mathbf{x}, z_j)} \, \mathrm{d}z_j - \int q_j(z_j) \, \text{log } q_j(z_j) \, \mathrm{d}z_j \\[.5em] &= \int q_j(z_j) \, \text{log } \frac{\tilde{p}{(\mathbf{x}, z_j)}}{q_j(z_j)} \, \mathrm{d}z_j \\[.5em] &= -\int q_j(z_j) \, \text{log } \frac{q_j(z_j)}{\tilde{p}{(\mathbf{x}, z_j)}} \, \mathrm{d}z_j \\[.5em] &= -\text{KL}\left(q_j(z_j) \, \lvert\lvert \, \tilde{p}(\mathbf{x}, z_j)\right) \enspace . \end{aligned}\]

Thus, maximizing the ELBO with respect to $q_j(z_j)$ is minimizing the Kullback-leibler divergence between $q_j(z_j)$ and $\tilde{p}(\mathbf{x}, z_j)$; it is zero when the two distributions are equal. Therefore, under the mean-field assumption, the optimal variational density $q_j^\star(z_j)$ is given by:

\[\begin{aligned} q_j^\star(z_j) &= \text{exp}\left(\mathbb{E}_{q_{-j}(\mathbf{z}_{-j})}\left[\text{log } p(\mathbf{x}, \mathbf{z}) \right] - \mathcal{Z}\right) \\[.5em] &= \frac{\text{exp}\left(\mathbb{E}_{q_{-j}(\mathbf{z}_{-j})}\left[\text{log } p(\mathbf{x}, \mathbf{z}) \right]\right)}{\int \text{exp}\left(\mathbb{E}_{q_{-j}(\mathbf{z}_{-j})}\left[\text{log } p(\mathbf{x}, \mathbf{z}) \right]\right) \mathrm{d}z_j} \enspace , \end{aligned}\]

see also Bishop (2006, p. 466). This is not an explicit solution, however, since each optimal variational density depends on all others. This calls for an iterative solution in which we first initialize all factors $q_j(z_i)$ and then cycle through them, updating them conditional on the updates of the other. Such a procedure is known as Coordinate Ascent Variational Inference (CAVI). Further, note that

\[p(z_j \mid \mathbf{z}_{-j}, \mathbf{x}) = \frac{p(z_j, \mathbf{z}_{-j}, \mathbf{x})}{p(\mathbf{z}_{-j}, \mathbf{x})} \propto p(z_j, \mathbf{z}_{-j}, \mathbf{x}) \enspace ,\]

which allows us to write the updates in terms of the conditional posterior distribution of $z_j$ given all other factors $\mathbf{z}_{-j}$. This looks a lot like Gibbs sampling, which we discussed in detail in a previous blog post. In the next section, we implement CAVI for a simple linear regression problem.

Application: Linear regression

In a previous blog post, we traced the history of least squares and applied it to the most basic problem: fitting a straight line to a number of points. Here, we study the same problem but swap optimization procedure: instead of least squares or maximum likelihood, we use variational inference. Our linear regression setup is:

\[\begin{aligned} y &\sim \mathcal{N}(\beta x, \sigma^2) \\[.5em] \beta &\sim \mathcal{N}(0, \sigma^2 \tau^2) \\[.5em] \sigma^2 &\propto \frac{1}{\sigma^2} \enspace , \end{aligned}\]

where we assume that the population mean of $y$ is zero (i.e., $\beta_0 = 0$); and we assign the error variance $\sigma^2$ an improper Jeffreys’ prior and $\beta$ a Gaussian prior with variance $\sigma^2\tau^2$. We scale the prior of $\beta$ by the error variance to reason in terms of a standardized effect size $\beta / \sigma$ since with this specification:

\[\text{Var}\left[\frac{\beta}{\sigma}\right] = \frac{1}{\sigma^2} \text{Var}[\beta] = \frac{\sigma^2 \tau^2}{\sigma^2} = \tau^2 \enspace .\]

As a heads up, we have to do a surprising amount of calculations to implement variational inference even for this simple problem. In the next section, we start our journey by deriving the variational density for $\sigma^2$.

Variational density for $\sigma^2$

Our optimal variational density $q^\star(\sigma^2)$ is given by:

\[q^\star(\sigma^2) \propto \text{exp}\left(\mathbb{E}_{q(\beta)}\left[\text{log } p(\sigma^2 \mid \mathbf{y}, \beta) \right]\right) \enspace .\]

To get started, we need to derive the conditional posterior distribution $p(\sigma^2 \mid \mathbf{y}, \beta)$. We write:

\[\begin{aligned} p(\sigma^2 \mid \mathbf{y}, \beta) &\propto p(\mathbf{y} \mid \sigma^2, \beta) \, p(\beta) \, p(\sigma^2) \\[.5em] &= \prod_{i=1}^n (2\pi)^{-\frac{1}{2}} \left(\sigma^2\right)^{-\frac{1}{2}} \text{exp}\left(-\frac{1}{2\sigma^2} \left(y_i - \beta x_i\right)^2\right) \underbrace{(2\pi)^{-\frac{1}{2}} \left(\sigma^2\tau^2\right)^{-\frac{1}{2}} \text{exp}\left(-\frac{1}{2\sigma^2\tau^2} \beta^2\right)}_{p(\beta)} \underbrace{\left(\sigma^2\right)^{-1}}_{p(\sigma^2)} \\[.5em] &= (2\pi)^{-\frac{n + 1}{2}} \left(\sigma^2\right)^{-\frac{n + 1}{2} - 1} \left(\tau^2\right)^{-1}\text{exp}\left(-\frac{1}{2\sigma^2} \left(\sum_{i=1}^n\left(y_i - \beta x_i\right)^2 + \frac{\beta^2}{\tau^2}\right)\right) \\[.5em] &\propto\left(\sigma^2\right)^{-\frac{n + 1}{2} - 1} \text{exp}\left(-\frac{1}{2\sigma^2} \underbrace{\left(\sum_{i=1}^n\left(y_i - \beta x_i\right)^2 + \frac{\beta^2}{\tau^2}\right)}_{A}\right) \enspace , \end{aligned}\]

which is proportional to an inverse Gamma distribution. Moving on, we exploit the linearity of the expectation and write:

\[\begin{aligned} q^\star(\sigma^2) &\propto \text{exp}\left(\mathbb{E}_{q(\beta)}\left[\text{log } p(\sigma^2 \mid \mathbf{y}, \beta) \right]\right) \\[.5em] &= \text{exp}\left(\mathbb{E}_{q(\beta)}\left[\text{log } \left(\sigma^2\right)^{-\frac{n+1}{2} - 1} - \frac{1}{2\sigma^2}A \right]\right) \\[.5em] &= \text{exp}\left(\mathbb{E}_{q(\beta)}\left[\text{log } \left(\sigma^2\right)^{-\frac{n+1}{2} - 1}\right] - \mathbb{E}_{q(\beta)}\left[\frac{1}{2\sigma^2}A \right]\right) \\[.5em] &= \text{exp}\left(\text{log } \left(\sigma^2\right)^{-\frac{n+1}{2} - 1} - \frac{1}{\sigma^2}\mathbb{E}_{q(\beta)}\left[\frac{1}{2}A \right]\right) \\[.5em] &= \left(\sigma^2\right)^{-\frac{n+1}{2} - 1} \text{exp}\left(-\frac{1}{\sigma^2}\mathbb{E}_{q(\beta)}\left[\frac{1}{2}A \right]\right) \enspace . \end{aligned}\]

This, too, looks like an inverse Gamma distribution! Plugging in the normalizing constant, we arrive at:

\[q^\star(\sigma^2)= \frac{\mathbb{E}_{q(\beta)}\left[\frac{1}{2}A \right]^{\frac{n + 1}{2}}}{\Gamma\left(\frac{n + 1}{2}\right)}\left(\sigma^2\right)^{-\frac{n + 1}{2} - 1} \text{exp}\left(-\frac{1}{\sigma^2} \underbrace{\mathbb{E}_{q(\beta)}\left[\frac{1}{2}A \right]}_{\nu}\right) \enspace .\]

Note that this quantity depends on $\beta$. In the next section, we derive the variational density for $\beta$.

Variational density for $\beta$

Our optimal variational density $q^\star(\beta)$ is given by:

\[q^\star(\beta) \propto \text{exp}\left(\mathbb{E}_{q(\sigma^2)}\left[\text{log } p(\beta \mid \mathbf{y}, \sigma^2) \right]\right) \enspace ,\]

and so we again have to derive the conditional posterior distribution $p(\beta \mid \mathbf{y}, \sigma^2)$. We write:

\[\begin{aligned} p(\beta \mid \mathbf{y}, \sigma^2) &\propto p(\mathbf{y} \mid \beta, \sigma^2) \, p(\beta) \, p(\sigma^2) \\[.5em] &= (2\pi)^{-\frac{n + 1}{2}} \left(\sigma^2\right)^{-\frac{n + 1}{2} - 1} \left(\tau^2\right)^{-1}\text{exp}\left(-\frac{1}{2\sigma^2} \left(\sum_{i=1}^n\left(y_i - \beta x_i\right)^2 + \frac{\beta^2}{\tau^2}\right)\right) \\[.5em] &= (2\pi)^{-\frac{n + 1}{2}} \left(\sigma^2\right)^{-\frac{n + 1}{2} - 1} \left(\tau^2\right)^{-1}\text{exp}\left(-\frac{1}{2\sigma^2} \left(\sum_{i=1}^ny_i^2- 2 \beta \sum_{i=1}^n y_i x_i + \beta^2 \sum_{i=1}^n x_i^2 + \frac{\beta^2}{\tau^2}\right)\right) \\[.5em] &\propto \text{exp}\left(-\frac{1}{2\sigma^2} \left( \beta^2 \left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right) - 2 \beta \sum_{i=1}^n y_i x_i\right)\right) \\[.5em] &=\text{exp}\left(-\frac{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}}{2\sigma^2} \left( \beta^2 - 2 \beta \frac{\sum_{i=1}^n y_i x_i}{\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)}\right)\right) \\[.5em] &\propto \text{exp}\left(-\frac{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}}{2\sigma^2} \left( \beta - \frac{\sum_{i=1}^n y_i x_i}{\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)}\right)^2\right) \enspace , \end{aligned}\]

where we have “completed the square” (see also this blog post) and realized that the conditional posterior is Gaussian. We continue by taking expectations:

\[\begin{aligned} q^\star(\beta) &\propto \text{exp}\left(\mathbb{E}_{q(\sigma^2)}\left[\text{log } p(\beta \mid \mathbf{y}, \sigma^2) \right]\right) \\[.5em] &= \text{exp}\left(\mathbb{E}_{q(\sigma^2)}\left[-\frac{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}}{2\sigma^2} \left( \beta - \frac{\sum_{i=1}^n y_i x_i}{\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)}\right)^2\right]\right) \\[.5em] &= \text{exp}\left(-\frac{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}}{2}\mathbb{E}_{q(\sigma^2)}\left[\frac{1}{\sigma^2}\right]\left( \beta - \frac{\sum_{i=1}^n y_i x_i}{\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)}\right)^2\right) \enspace , \end{aligned}\]

which is again proportional to a Gaussian distribution! Plugging in the normalizing constant yields:

\[q^\star(\beta) = \left(2\pi\underbrace{\frac{\mathbb{E}_{q(\sigma^2)}\left[\frac{1}{\sigma^2}\right]^{-1}}{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}}}_{\sigma^2_{\beta}}\right)^{-\frac{1}{2}} \text{exp}\left(-\frac{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}}{2}\mathbb{E}_{q(\sigma^2)}\left[\frac{1}{\sigma^2}\right]\left(\beta - \underbrace{\frac{\sum_{i=1}^n y_i x_i}{\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)}}_{\mu_{\beta}}\right)^2\right) \enspace ,\]

Note that while the variance of this distribution, $\sigma^2_\beta$, depends on $q(\sigma^2)$, its mean $\mu_\beta$ does not.

To recap, instead of assuming a parametric form for the variational densities, we have derived the optimal densities under the mean-field assumption, that is, under the assumption that the parameters are independent: $q(\beta, \sigma^2) = q(\beta) \, q(\sigma^2)$. Assigning $\beta$ a Gaussian distribution and $\sigma^2$ a Jeffreys’s prior, we have found that the variational density for $\sigma^2$ is an inverse Gamma distribution and that the variational density for $\beta$ a Gaussian distribution. We noted that these variational densities depend on each other. However, this is not the end of the manipulation of symbols; both distributions still feature an expectation we need to remove. In the next section, we expand the remaining expectations.

Removing expectations

Now that we know the parametric form of both variational densities, we can expand the terms that involve an expectation. In particular, to remove the expectation in the variational density for $\sigma^2$, we write:

\[\begin{aligned} \mathbb{E}_{q(\beta)}\left[A \right] &= \mathbb{E}_{q(\beta)}\left[\left(\sum_{i=1}^n\left(y_i - \beta x_i\right)^2 + \frac{\beta^2}{\tau^2}\right)\right] \\[.5em] &= \sum_{i=1}^n y_i^2- 2 \sum_{i=1}^n y_i x_i \, \mathbb{E}_{q(\beta)}\left[\beta\right] + \sum_{i=1}^n x_i^2 \, \mathbb{E}_{q(\beta)}\left[\beta^2\right] + \frac{1}{\tau^2} \, \mathbb{E}_{q(\beta)}\left[\beta^2\right] \enspace . \end{aligned}\]

Noting that $\mathbb{E}_{q(\beta)}[\beta] = \mu_{\beta}$ and using the fact that:

\[\mathbb{E}_{q(\beta)}[\beta^2] = \text{Var}_{q(\beta)}\left[\beta\right] + \mathbb{E}_{q(\beta)}[\beta]^2 = \sigma^2_{\beta} + \mu_{\beta}^2 \enspace ,\]

the expectation becomes:

\[\mathbb{E}_{q(\beta)}\left[A\right] = \sum_{i=1}^n y_i^2- 2 \sum_{i=1}^n y_i x_i \, \mu_{\beta} + \left(\sigma^2_{\beta} + \mu_{\beta}^2\right)\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right) \enspace .\]

For the expectation which features in the variational distribution for $\beta$, things are slightly less elaborate, although the result also looks unwieldy. We write:

\[\begin{aligned} \mathbb{E}_{q(\sigma^2)}\left[\frac{1}{\sigma^2}\right] &= \int \frac{1}{\sigma^2}\frac{\nu^{\frac{n + 1}{2}}}{\Gamma\left(\frac{n + 1}{2}\right)}\left(\sigma^2\right)^{-\frac{n + 1}{2} - 1} \text{exp}\left(-\frac{1}{\sigma^2} \nu\right) \mathrm{d}\sigma^2\\[0.50em] &= \frac{\nu^{\frac{n + 1}{2}}}{\Gamma\left(\frac{n + 1}{2}\right)} \int \left(\sigma^2\right)^{-\left(\frac{n + 1}{2} + 1\right) - 1} \text{exp}\left(-\frac{1}{\sigma^2} \nu\right) \mathrm{d}\sigma^2 \\[0.50em] &= \frac{\nu^{\frac{n + 1}{2}}}{\Gamma\left(\frac{n + 1}{2}\right)} \frac{\Gamma\left(\frac{n + 1}{2} + 1\right)}{\nu^{\frac{n + 1}{2} + 1}} \\[0.50em] &= \frac{n + 1}{2} \left(\frac{1}{2}\mathbb{E}_{q(\beta)}\left[A \right]\right)^{-1} \\[.5em] &= \frac{n + 1}{2} \left(\frac{1}{2}\left(\sum_{i=1}^n y_i^2- 2 \sum_{i=1}^n y_i x_i \, \mu_{\beta} + \left(\sigma^2_{\beta} + \mu_{\beta}^2\right)\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)\right)\right)^{-1} \enspace . \end{aligned}\]

Monitoring convergence

The algorithm works by first specifying initial values for the parameters of the variational densities and then iteratively updating them until the ELBO does not change anymore. This requires us to compute the ELBO, which we still need to derive, on each update. We write:

\[\begin{aligned} \text{ELBO}(q) &= \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } p(\mathbf{y}, \beta, \sigma^2)\right] - \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } q(\beta, \sigma^2) \right] \\[.5em] &= \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } p(\mathbf{y} \mid \beta, \sigma^2)\right] + \mathbb{E}_{p(\beta, \sigma^2)}\left[\text{log } p(\beta, \sigma^2)\right] - \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } q(\beta, \sigma^2)\right] \\[.5em] &= \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } p(\mathbf{y} \mid \beta, \sigma^2)\right] + \underbrace{\mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } \frac{p(\beta, \sigma^2)}{q(\beta, \sigma^2)}\right]}_{-\text{KL}\left(q(\beta, \sigma^2) \, \lvert\lvert \, p(\beta, \sigma^2)\right)}\enspace . \end{aligned}\]

Let’s take a deep breath and tackle the second term first:

\[\begin{aligned} \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } \frac{p(\beta, \sigma^2)}{q(\beta, \sigma^2)}\right] &= \mathbb{E}_{q(\sigma^2)}\left[\mathbb{E}_{q(\beta)}\left[\text{log } \frac{p(\beta \mid \sigma^2)}{q(\beta)}\right] + \text{log } \frac{p(\sigma^2)}{q(\sigma^2)}\right] \\[.5em] &= \mathbb{E}_{q(\sigma^2)}\left[\mathbb{E}_{q(\beta)}\left[\text{log } \frac{\left(2\pi\sigma^2\tau^2\right)^{-\frac{1}{2}}\text{exp}\left(-\frac{1}{2\sigma^2\tau^2} \beta^2\right)}{\left(2\pi\sigma^2_\beta\right)^{-\frac{1}{2}}\text{exp}\left(-\frac{1}{2\sigma^2_\beta} (\beta - \mu_\beta)^2\right)}\right] + \text{log } \frac{p(\sigma^2)}{q(\sigma^2)}\right] \\[.5em] &= \mathbb{E}_{q(\sigma^2)}\left[\mathbb{E}_{q(\beta)}\left[\text{log } \frac{\sigma^2\tau^2}{\sigma^2_\beta} + \frac{\frac{1}{\sigma^2\tau^2} \beta^2}{\frac{1}{\sigma^2_\beta} (\beta - \mu_\beta)^2}\right] + \text{log } \frac{p(\sigma^2)}{q(\sigma^2)}\right] \\[.5em] &= \mathbb{E}_{q(\sigma^2)}\left[\text{log}\frac{\sigma^2\tau^2}{\sigma^2_\beta} + \frac{\sigma^2_\beta + \mu_\beta^2}{\sigma^2\tau^2}\right] + \mathbb{E}_{q(\sigma^2)}\left[\text{log } \frac{p(\sigma^2)}{q(\sigma^2)}\right] \\[.5em] &= \text{log}\frac{\tau^2}{\sigma^2_\beta} + \mathbb{E}_{q(\sigma^2)}\left[\text{log }\sigma^2\right] + \frac{\sigma^2_\beta + \mu_\beta^2}{\tau^2}\mathbb{E}_{q(\sigma^2)}\left[\frac{1}{\sigma^2}\right] + \mathbb{E}_{q(\sigma^2)}\left[\text{log } \frac{p(\sigma^2)}{q(\sigma^2)}\right] \\[.5em] &= \text{log}\frac{\tau^2}{\sigma^2_\beta} + \mathbb{E}_{q(\sigma^2)}\left[\text{log }\sigma^2\right] + \frac{\sigma^2_\beta + \mu_\beta^2}{\tau^2}\mathbb{E}_{q(\sigma^2)}\left[\frac{1}{\sigma^2}\right] + \mathbb{E}_{q(\sigma^2)}\left[\text{log } p(\sigma^2)\right] - \mathbb{E}_{q(\sigma^2)}\left[\text{log } q(\sigma^2)\right]\enspace . \end{aligned}\]

Note that there are three expectations left. However, we really deserve a break, and so instead of analytically deriving the expectations we compute $\mathbb{E}_{q(\sigma^2)}\left[\text{log } \sigma^2\right]$ and $\mathbb{E}_{p(\sigma^2)}\left[\text{log } q(\sigma^2)\right]$ numerically using Gaussian quadrature. This fails for $\mathbb{E}_{q(\sigma^2)}\left[\text{log } q(\sigma^2)\right]$, which we compute using Monte carlo integration:

\[\mathbb{E}_{q(\sigma^2)}\left[\text{log } q(\sigma^2)\right] = \int q(\sigma^2) \, \text{log } q(\sigma^2) \, \mathrm{d}\sigma^2 \approx \frac{1}{N} \sum_{i=1}^N \underbrace{\text{log } q(\sigma^2)}_{\sigma^2 \, \sim \, q(\sigma^2)} \enspace ,\]

We are left with the expected log likelihood. Instead of filling this blog post with more equations, we again resort to numerical methods. However, we refactor the expression so that numerical integration is more efficient:

\[\begin{aligned} \mathbb{E}_{q(\beta, \sigma^2)}\left[\text{log } p(\mathbf{y} \mid \beta, \sigma^2)\right] &= \int \int q(\beta) \, q(\sigma^2) \, \text{log } p(\mathbf{y} \mid \beta, \sigma^2) \, \mathrm{d}\sigma \mathrm{d}\beta \\[.5em] &=\int q(\beta) \int q(\sigma^2) \, \text{log} \left(\left(2\pi\sigma^2\right)^{-\frac{n}{2}}\text{exp}\left(-\frac{1}{2\sigma^2} \sum_{i=1}^n (y_i - x_i\beta)^2\right)\right) \, \mathrm{d}\sigma \mathrm{d}\beta \\[.5em] &= \frac{n}{4} \text{log}\left(2\pi\right)\int q(\beta) \left(\sum_{i=1}^n (y_i - x_i\beta)^2\right) \, \mathrm{d}\beta\int q(\sigma^2) \, \, \text{log} \left(\sigma^2\right)\frac{1}{\sigma^2} \, \mathrm{d}\sigma \enspace . \end{aligned}\]

Since we have solved a similar problem already above, we evaluate the expecation with respect to $q(\beta)$ analytically:

\[\mathbb{E}_{q(\beta)}\left[\sum_{i=1}^n (y_i - x_i\beta)^2\right] = \sum_{i=1}^n y_i^2- 2 \sum_{i=1}^n y_i x_i \, \mu_{\beta} + \left(\sigma^2_{\beta} + \mu_{\beta}^2\right)\left(\sum_{i=1}^n x_i^2\right) \enspace .\]

In the next section, we implement the algorithm for our linear regression problem in R.

Implementation in R

Now that we have derived the optimal densities, we know how they are parameterized. Therefore, the ELBO is a function of these variational parameters and the parameters of the priors, which in our case is just $\tau^2$. We write a function that computes the ELBO:

library('MCMCpack')
 
#' Computes the ELBO for the linear regression example
#' 
#' @param y univariate outcome variable
#' @param x univariate predictor variable
#' @param beta_mu mean of the variational density for \beta
#' @param beta_sd standard deviation of the variational density for \beta
#' @param nu parameter of the variational density for \sigma^2
#' @param nr_samples number of samples for the Monte carlo integration
#' @returns ELBO
compute_elbo <- function(y, x, beta_mu, beta_sd, nu, tau2, nr_samples = 1e4) {
  n <- length(y)
  sum_y2 <- sum(y^2)
  sum_x2 <- sum(x^2)
  sum_yx <- sum(x*y)
  
  # Takes a function and computes its expectation with respect to q(\beta)
  E_q_beta <- function(fn) {
    integrate(function(beta) {
      dnorm(beta, beta_mu, beta_sd) * fn(beta)
    }, -Inf, Inf)$value
  }
  
  # Takes a function and computes its expectation with respect to q(\sigma^2)
  E_q_sigma2 <- function(fn) {
    integrate(function(sigma) {
      dinvgamma(sigma^2, (n + 1)/2, nu) * fn(sigma)
    }, 0, Inf)$value
  }
  
  
  # Compute expectations of log p(\sigma^2)
  E_log_p_sigma2 <- E_q_sigma2(function(sigma) log(1/sigma^2))
  
  # Compute expectations of log p(\beta \mid \sigma^2)
  E_log_p_beta <- (
    log(tau2 / beta_sd^2) * E_q_sigma2(function(sigma) log(sigma^2)) +
    (beta_sd^2 + tau2) / (tau2) * E_q_sigma2(function(sigma) 1/sigma^2)
  )
  
  # Compute expectations of the log variational densities q(\beta)
  E_log_q_beta <- E_q_beta(function(beta) dnorm(beta, beta_mu, beta_sd, log = TRUE))
  # E_log_q_sigma2 <- E_q_sigma2(function(x) log(dinvgamma(x, (n + 1)/2, nu))) # fails
  
  # Compute expectations of the log variational densities q(\sigma^2)
  sigma2 <- rinvgamma(nr_samples, (n + 1)/2, nu)
  E_log_q_sigma2 <- mean(log(dinvgamma(sigma2, (n + 1)/2, nu)))
  
  
  # Compute the expected log likelihood
  E_log_y_b <- sum_y2 - 2*sum_yx*beta_mu + (beta_sd^2 + beta_mu^2)*sum_x2
  E_log_y_sigma2 <- E_q_sigma2(function(sigma) log(sigma^2) * 1/sigma^2)
  E_log_y <- n/4 * log(2*pi) * E_log_y_b * E_log_y_sigma2
  
  
  # Compute and return the ELBO
  ELBO <- E_log_y + E_log_p_beta + E_log_p_sigma2 - E_log_q_beta - E_log_q_sigma2
  ELBO
}

The function below implements coordinate ascent mean-field variational inference for our simple linear regression problem. Recall that the variational parameters are:

\[\begin{aligned} \nu &= \frac{1}{2}\left(\sum_{i=1}^n y_i^2- 2 \sum_{i=1}^n y_i x_i \, \mu_{\beta} + \left(\sigma^2_{\beta} + \mu_{\beta}^2\right)\left(\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}\right)\right) \\[.5em] \mu_\beta &= \frac{\sum_{i=1}^N y_i x_i}{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}} \\[.5em] \sigma^2_\beta &= \frac{\left(\frac{n + 1}{2}\right) \nu^{-1}}{\sum_{i=1}^n x_i^2 + \frac{1}{\tau^2}} \enspace . \end{aligned}\]

The following function implements the iterative updating of these variational parameters until the ELBO has converged.

#' Implements CAVI for the linear regression example
#' 
#' @param y univariate outcome variable
#' @param x univariate predictor variable
#' @param tau2 prior variance for the standardized effect size
#' @returns parameters for the variational densities and ELBO
lmcavi <- function(y, x, tau2, nr_samples = 1e5, epsilon = 1e-2) {
  n <- length(y)
  sum_y2 <- sum(y^2)
  sum_x2 <- sum(x^2)
  sum_yx <- sum(x*y)
  
  # is not being updated through variational inference!
  beta_mu <- sum_yx / (sum_x2 + 1/tau2)
  
  res <- list()
  res[['nu']] <- 5
  res[['beta_mu']] <- beta_mu
  res[['beta_sd']] <- 1
  res[['ELBO']] <- 0
  
  j <- 1
  has_converged <- function(x, y) abs(x - y) < epsilon
  ELBO <- compute_elbo(y, x, beta_mu, 1, 5, tau2, nr_samples = nr_samples)
  
  # while the ELBO has not converged
  while (!has_converged(res[['ELBO']][j], ELBO)) {
    
    nu_prev <- res[['nu']][j]
    beta_sd_prev <- res[['beta_sd']][j]
    
    # used in the update of beta_sd and nu
    E_qA <- sum_y2 - 2*sum_yx*beta_mu + (beta_sd_prev^2 + beta_mu^2)*(sum_x2 + 1/tau2)
    
    # update the variational parameters for sigma2 and beta
    nu <- 1/2 * E_qA
    beta_sd <- sqrt(((n + 1) / E_qA) / (sum_x2 + 1/tau2))
    
    # update results object
    res[['nu']] <- c(res[['nu']], nu)
    res[['beta_sd']] <- c(res[['beta_sd']], beta_sd)
    res[['ELBO']] <- c(res[['ELBO']], ELBO)
    
    # compute new ELBO
    j <- j + 1
    ELBO <- compute_elbo(y, x, beta_mu, beta_sd, nu, tau2, nr_samples = nr_samples)
  }
  
  res
}

Let’s run this on a simulated data set of size $n = 100$ with a true coefficient of $\beta = 0.30$ and a true error variance of $\sigma^2 = 1$. We assign $\beta$ a Gaussian prior with variance $\tau^2 = 0.25$ so that values for $\lvert \beta \rvert$ larger than two standard deviations ($0.50$) receive about $0.68$ prior probability.

gen_dat <- function(n, beta, sigma) {
  x <- rnorm(n)
  y <- 0 + beta*x + rnorm(n, 0, sigma)
  data.frame(x = x, y = y)
}
 
set.seed(1)
dat <- gen_dat(100, 0.30, 1)
 
mc <- lmcavi(dat$y, dat$x, tau2 = 0.50^2)
mc

## $nu
## [1]  5.00000 88.17995 45.93875 46.20205 46.19892 46.19895
## 
## $beta_mu
## [1] 0.2800556
## 
## $beta_sd
## [1] 1.00000000 0.08205605 0.11368572 0.11336132 0.11336517 0.11336512
## 
## $ELBO
## [1]       0.0000 -297980.0495     493.4807    -281.4578    -265.1289    -265.3197

From the output, we see that the ELBO and the variational parameters have converged. In the next section, we compare these results to results obtained with Stan.

Comparison with Stan

Whenever one goes down a rabbit hole of calculations, it is good to sanity check one’s results. Here, we use Stan’s variational inference scheme to check whether our results are comparable. It assumes a Gaussian variational density for each parameter after transforming them to the real line and automates inference in a “black-box” way so that no problem-specific calculations are required (see Kucukelbir, Ranganath, Gelman, & Blei, 2015). Subsequently, we compare our results to the exact posteriors arrived by Markov chain Monte carlo. The simple linear regression model in Stan is:

data {
  int<lower=0> n;
  vector[n] y;
  vector[n] x;
  real tau;
}
 
parameters {
  real b;
  real<lower=0> sigma;
}
 
model {
  target += -log(sigma);
  target += normal_lpdf(b | 0, sigma*tau);
  target += normal_lpdf(y | b*x, sigma);
}

We use Stan’s black-box variational inference scheme:

library('rstan')
 
# save the above model to a file and compile it
model <- stan_model(file = 'stan-compiled/variational-regression.stan')
 
stan_dat <- list('n' = nrow(dat), 'x' = dat$x, 'y' = dat$y, 'tau' = 0.50)
fit <- vb(
  model, data = stan_dat, output_samples = 20000, adapt_iter = 10000,
  init = list('b' = 0.30, 'sigma' = 1), refresh = FALSE, seed = 1
)

This gives similar estimates as ours:

fit

## Inference for Stan model: variational-regression.
## 1 chains, each with iter=20000; warmup=0; thin=1; 
## post-warmup draws per chain=20000, total post-warmup draws=20000.
## 
##       mean   sd 2.5%  25%  50%  75% 97.5%
## b     0.28 0.13 0.02 0.19 0.28 0.37  0.54
## sigma 0.99 0.09 0.82 0.92 0.99 1.05  1.18
## lp__  0.00 0.00 0.00 0.00 0.00 0.00  0.00
## 
## Approximate samples were drawn using VB(meanfield) at Thu Mar 19 10:45:28 2020.

## We recommend genuine 'sampling' from the posterior distribution for final inferences!

Their recommendation is prudent. If you run the code with different seeds, you can get quite different results. For example, the posterior mean of $\beta$ can range from $0.12$ to $0.45$, and the posterior standard deviation can be as low as $0.03$; in all these settings, Stan indicates that the ELBO has converged, but it seems that it has converged to a different local optimum for each run. (For seed = 3, Stan gives completely nonsensical results). Stan warns that the algorithm is experimental and may be unstable, and it is probably wise to not use it in production.

Update: As Ben Goodrich points out in the comments, there is some cool work on providing diagnostics for variational inference; see this blog post and the paper by Yao, Vehtari, Simpson, & Gelman (2018) as well as the paper by Huggins, Kasprzak, Campbell, & Broderik (2019).

Although the posterior distribution for $\beta$ and $\sigma^2$ is available in closed-form (see the Post Scriptum), we check our results against exact inference using Markov chain Monte carlo by visual inspection.

fit <- sampling(model, data = stan_dat, iter = 8000, refresh = FALSE, seed = 1)

The Figure below overlays our closed-form results to the histogram of posterior samples obtained using Stan.

plot of chunk unnamed-chunk-10

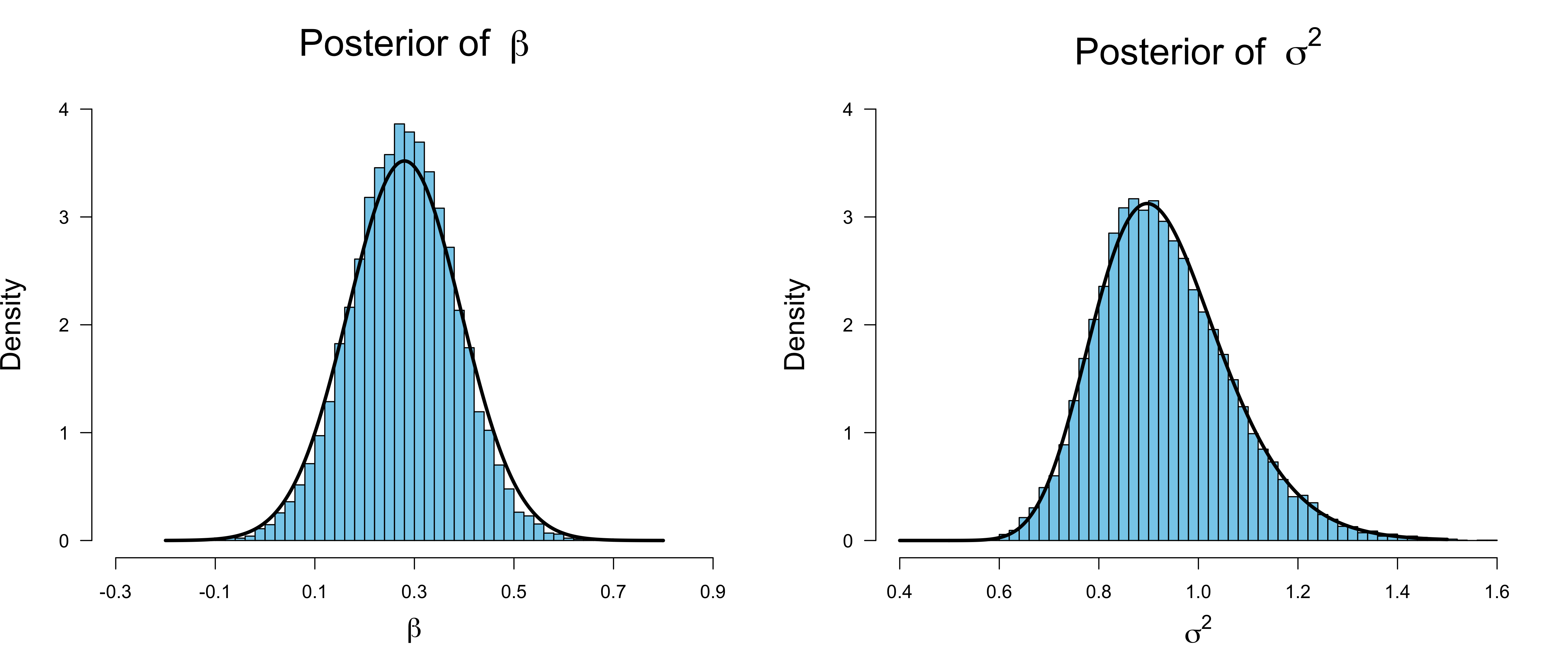
Note that the posterior variance of $\beta$ is slightly overestimated when using our variational scheme. This is in contrast to the fact that variational inference generally underestimates variances. Note also that Bayesian inference using Markov chain Monte Carlo is very fast on this simple problem. However, the comparative advantage of variational inference becomes clear by increasing the sample size: for sample sizes as large as $n = 100000$, our variational inference scheme takes less then a tenth of a second!

Conclusion

In this blog post, we have seen how to turn an integration problem into an optimization problem using variational inference. Assuming that the variational densities are independent, we have derived the optimal variational densities for a simple linear regression problem with one predictor. While using variational inference for this problem is unnecessary since everything is available in closed-form, I have focused on such a simple problem so as to not confound this introduction to variational inference by the complexity of the model. Still, the derivations were quite lengthy. They were also entirely specific to our particular problem, and thus generic “black-box” algorithms which avoid problem-specific calculations hold great promise.

We also implemented coordinate ascent mean-field variational inference (CAVI) in R and compared our results to results obtained via variational and exact inference using Stan. We have found that one probably should not trust Stan’s variational inference implementation, and that our results closely correspond to the exact procedure. For more on variational inference, I recommend the excellent review article by Blei, Kucukelbir, and McAuliffe (2017).

I would like to thank Don van den Bergh for helpful comments on this blog post.

Post Scriptum

Normal-inverse-gamma Distribution

The posterior distribution is a Normal-inverse-gamma distribution:

\[p(\beta, \sigma^2 \mid \mathbf{y}) = \frac{\gamma^{\alpha}}{\Gamma\left(\alpha\right)} \left(\sigma^2\right)^{-\alpha - 1} \text{exp}\left(-\frac{2\gamma + \lambda\left(\beta - \mu\right)^2}{2\sigma^2}\right) \enspace ,\]

where

\[\begin{aligned} \mu &= \frac{\sum_{i=1}^n y_i x_i}{\sum_{i=1}^n x_i + \frac{1}{\tau^2}} \\[.5em] \lambda &= \sum_{i=1}^n x_i + \frac{1}{\tau^2} \\[.5em] \alpha &= \frac{n + 1}{2} \\[.5em] \gamma &= \left(\frac{1}{2}\left(\sum_{i=1}^n y_i^2 - \frac{\left(\sum_{i=1}^n y_i x_i\right)^2}{\sum_{i=1}^n x_i + \frac{1}{\tau^2}}\right)\right) \enspace . \end{aligned}\]

Note that the marginal posterior distribution for $\beta$ is actually a Student-t distribution, contrary to what we assume in our variational inference scheme.

References

Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational inference: A review for statisticians. Journal of the American Statistical Association, 112(518), 859-877.
Huggins, J. H., Kasprzak, M., Campbell, T., & Broderick, T. (2019). Practical Posterior Error Bounds from Variational Objectives. arXiv preprint arXiv:1910.04102.
Kucukelbir, A., Ranganath, R., Gelman, A., & Blei, D. (2015). Automatic variational inference in Stan. In Advances in Neural Information Processing Systems (pp. 568-576).
Kucukelbir, A., Tran, D., Ranganath, R., Gelman, A., & Blei, D. M. (2017). Automatic differentiation variational inference. The Journal of Machine Learning Research, 18(1), 430-474.
Yao, Y., Vehtari, A., Simpson, D., & Gelman, A. (2018). Yes, but did it work?: Evaluating variational inference. arXiv preprint arXiv:1802.02538.

Footnotes

The first part of this blog post draws heavily on the excellent review article by Blei, Kucukelbier, and McAuliffe (2017), and so I use their (machine learning) notation. ↩

Written on October 30th, 2019 by Fabian Dablander

Feel free to share!