Fabian Dablander Postdoc Behavioural Data Science & Sustainability
Infectious diseases and nonlinear differential equations
Last summer, I wrote about love affairs and linear differential equations. While the topic is cheerful, linear differential equations are severely limited in the types of behaviour they can model. In this blog post, which I spent writing in self-quarantine to prevent further spread of SARS-CoV-2 — take that, cheerfulness — I introduce nonlinear differential equations as a means to model infectious diseases. In particular, we will discuss the simple SIR and SIRS models, the building blocks of many of the more complicated models used in epidemiology.
Before doing so, however, I discuss some of the basic tools of nonlinear dynamics applied to the logistic equation as a model for population growth. If you are already familiar with this, you can skip ahead. If you have had no prior experience with differential equations, I suggest you first check out my earlier post on the topic.
I should preface this by saying that I am not an epidemiologist, and that no analysis I present here is specifically related to the current SARS-CoV-2 pandemic, nor should anything I say be interpreted as giving advice or making predictions. I am merely interested in differential equations, and as with love affairs, infectious diseases make a good illustrating case. So without further ado, let’s dive in!
Modeling Population Growth
Before we start modeling infectious diseases, it pays to study the concepts required to study nonlinear differential equations on a simple example: modeling population growth. Let $N > 0$ denote the size of a population and assume that its growth depends on itself:
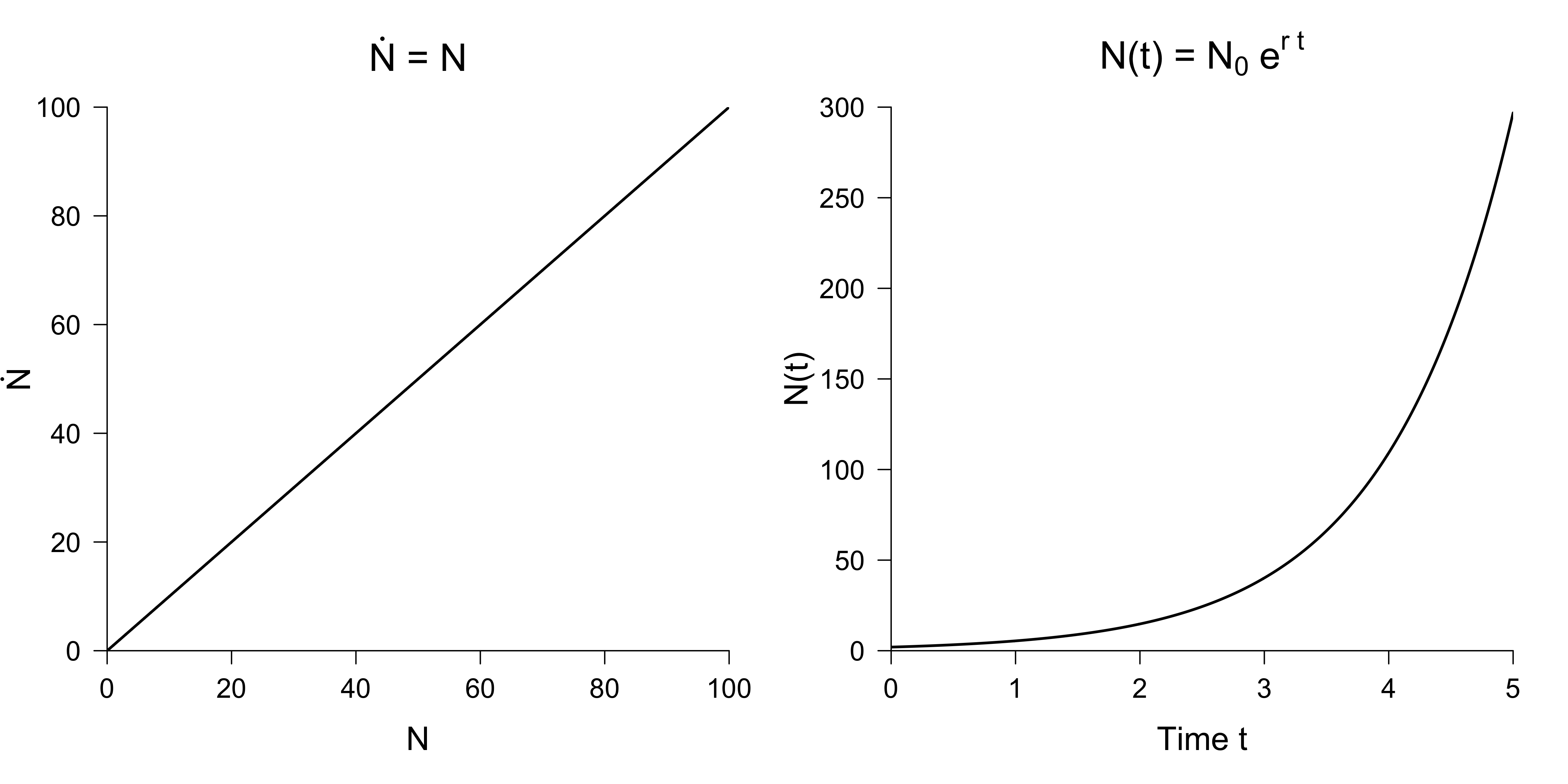
\[\frac{dN}{dt} = \dot{N} = r N \enspace .\]As shown in a previous blog post, this leads to exponential growth for $r > 0$:
\[N(t) = N_0 e^{r t} \enspace ,\]where $N_0 = N(0)$ is the initial population size at time $t = 0$. The figure below visualizes the differential equation (left panel) and its solution (right panel) for $r = 1$ and an initial population of $N_0 = 2$.
This is clearly not a realistic model since the growth of a population depends on resources, which are finite. To model finite resources, we write:
\[\dot{N} = rN \left(1 - \frac{N}{K}\right) \enspace ,\]where $r > 0$ and $K$ is the so-called carrying capacity, that is, the maximum sized population that can be sustained by the available resources. Observe that as $N$ grows and if $K > N$, then $(1 - N / K)$ gets smaller, slowing down the growth rate $\dot{N}$. If on the other hand $N > K$, then the population needs more resources than are available, and the growth rate becomes negative, resulting in population decrease.
For simplicity, let $K = 1$ and interpret $N \in [0, 1]$ as the proportion with respect to the carrying capacity; that is, $N = 1$ implies that we are at carrying capacity. The figure below visualizes the differential equation and its solution for $r = 1$ and an initial condition $N_0 = 0.10$.
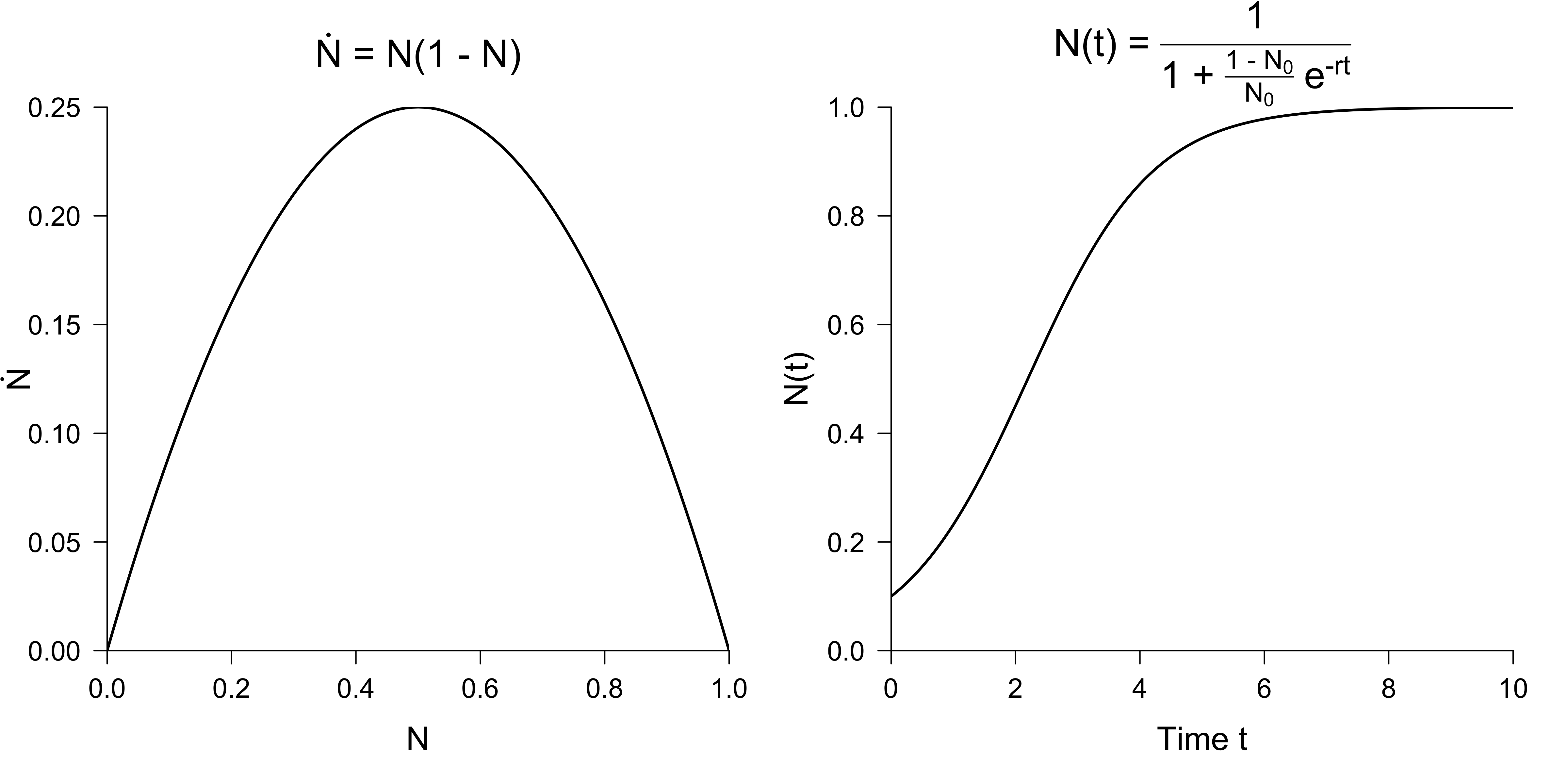
In contrast to exponential growth, the logistic equation leads to sigmoidal growth which approaches the carrying capacity. This is much more interesting behaviour than the linear differential equation above allows. In particular, the logistic equation has two fixed points — points at which the population neither increases nor decreases but stays fixed, that is, where $\dot{N} = 0$. These occur at $N = 0$ and at $N = 1$, as can be inferred from the left panel in the figure above.
Analyzing the Stability of Fixed Points
What is the stability of these fixed points? Intuitively, $N = 0$ should be unstable; if there are individuals, then they procreate and the population increases. Similarly, $N = 1$ should be stable: if $N < 1$, then $\dot{N} > 0$ and the population grows towards $N = 1$, and if $N > 1$, then $\dot{N} < 0$ and individuals die until $N = 1$.
To make this argument more rigorous, and to get a more quantitative assessment of how quickly perturbations move away from or towards a fixed point, we derive a differential equation for these small perturbations close to the fixed point (see also Strogatz, 2015, p. 24). Let $N^{\star}$ denote a fixed point and define $\eta(t) = N(t) - N^{\star}$ to be a small perturbation close to the fixed point. We derive a differential equation for $\eta$ by writing:
\[\frac{d\eta}{dt} = \frac{d}{dt}\left(N(t) - N^{\star}\right) = \frac{dN}{dt} \enspace ,\]since $N^{\star}$ is a constant. This implies that the dynamics of the perturbation equal the dynamics of the population. Let $f(N)$ denote the differential equation for $N$, observe that $N = N^{\star} + \eta$ such that $\dot{N} = \dot{\eta} = f(N) = f(N^{\star} + \eta)$. Recall that $f$ is a nonlinear function, and nonlinear functions are messy to deal with. Thus, we simply pretend that the function is linear close to the fixed point. More precisely, we approximate $f$ around the fixed point using a Taylor series (see this excellent video for details) by writing:
\[f(N^{\star} + \eta) = f(N^{\star}) + \eta f'(N^{\star}) + \mathcal{O}(\eta^2) \enspace ,\]where we have ignored higher order terms. Note that, by definition, there is no change at the fixed point, that is, $f(N^{\star}) = 0$. Assuming that $f’(N^{\star}) \neq 0$ — as otherwise the higher-order terms matter, as there would be nothing else — we have that close to a fixed point
\[\dot{\eta} \approx \eta f'(N^{\star}) \enspace ,\]which is a linear differential equation with solution:
\[\eta(t) = \eta_0 e^{f'(N^{\star})t} \enspace .\]Using this trick, we can assess the stability of $N^{\star}$ as follows. If $f’(N^{\star}) < 0$, the small perturbation $\eta(t)$ around the fixed point decays towards zero, and so the system returns to the fixed point — the fixed point is stable. On the other hand, if $f’(N^{\star}) > 0$, then the small perturbation $\eta(t)$ close to the fixed point grows, and so the system does not return to the fixed point — the fixed point is unstable. Applying this to our logistic equation, we see that:
\[\begin{aligned} f'(N) &= \frac{d}{dN} \left(rN(1 - N)\right) \\[0.50em] &= \frac{d}{dN} \left(rN - rN^2\right) \\[0.50em] & = r - 2rN \\[0.50em] &= r(1 - 2N) \enspace . \end{aligned}\]Plugging in our two fixed points $N^{\star} = 0$ and $N^{\star} = 1$, we find that $f’(0) = r$ and $f’(1) = -r$. Since $r > 0$, this confirms our suspicion that $N^{\star} = 0$ is unstable and $N^{\star} = 1$ is stable. In addition, this analysis tells us how quickly the perturbations grow or decay; for the logistic equation, this is given by $r$.
In sum, we have linearized a nonlinear system close to fixed points in order to assess the stability of these fixed points, and how quickly perturbations close to these fixed points grow or decay. This technique is called linear stability analysis. In the next two sections, we discuss two ways to solve differential equations using the logistic equation as an example.
Analytic Solution
In contrast to linear differential equations, which was the topic of a previous blog post, nonlinear differential equations can usually not be solved analytically; that is, we generally cannot get an expression that, given an initial condition, tells us the state of the system at any time point $t$. The logistic equation can, however, be solved analytically and it might be instructive to see how. We write:
\[\begin{aligned} \frac{dN}{dt} &= rN (1 - N) \\ \frac{dN}{N(1 - N)} &= r dt \\ \int \frac{1}{N(1 - N)} dN &= r t \enspace . \end{aligned}\]Staring at this for a bit, we realize that we can use partial fractions to split the integral. We write:
\[\begin{aligned} \int \frac{1}{N(1 - N)} dN &= r t \\[0.50em] \int \frac{1}{N} dN + \int \frac{1}{1 - N}dN &= rt \\[0.50em] \text{log}N - \text{log}(1 - N) + Z &= rt \\[0.50em] e^{\text{log}N - \text{log}(1 - N) + Z} &= e^{rt} \enspace . \end{aligned}\]The exponents and the logs cancel each other nicely. We write:
\[\begin{aligned} \frac{e^{\text{log}N}}{e^{\text{log}(1 - N)}}e^Z &= e^{rt} \\[0.50em] \frac{N}{1 - N} e^Z &= e^{rt} \\[0.50em] \frac{N}{1 - N} &= e^{rt - Z} \\[0.50em] N &= e^{rt - Z} - N e^{rt - Z} \\[0.50em] N\left(1 + e^{rt - Z}\right) &= e^{rt - Z} \\[0.50em] N &= \frac{e^{rt - Z}}{1 + e^{rt - Z}} \enspace . \end{aligned}\]One last trick is to multiply by $e^{-rt + Z}$, which yields:
\[N = \frac{\left(e^{-rt + Z}\right)\left(e^{rt - Z}\right)}{\left(e^{-rt + Z}\right) + {\left(e^{-rt + Z}\right)\left(e^{-rt + Z}\right)}} = \frac{1}{1 + e^{-rt + Z}} \enspace ,\]where $Z$ is the constant of integration. To solve for it, we need the initial condition. Suppose that $N(0) = N_0$, which, using the third line in the derivation above and the fact that $t = 0$, leads to:
\[\begin{aligned} \text{log}N_0 - \text{log}(1 - N_0) + Z &= 0 \\[0.50em] \text{log}N_0 - \text{log}(1 - N_0) &= -Z \\[0.50em] \frac{N_0}{1 - N_0} = e^{-Z} \\[0.50em] \frac{1 - N_0}{N_0} = e^{Z} \enspace . \end{aligned}\]Plugging this into our solution from above yields:
\[N(t) = \frac{1}{1 + e^{-rt + Z}} = \frac{1}{1 + \frac{1 - N_0}{N_0} e^{-rt}} \enspace .\]While this was quite a hassle, other nonlinear differential equations are much, much harder to solve, and most do not admit a closed-form solution — or at least if they do, the resulting expression is generally not very intuitive. Luckily, we can compute the time-evolution of the system using numerical methods, as illustrated in the next section.
Numerical Solution
A differential equation implicitly encodes how the system we model changes over time. Specifically, given a particular (potentially high-dimensional) state of the system at time point $t$, $\mathbf{x}_t$, we know in which direction and how quickly the system will change because this is exactly what is encoded in the differential equation $f = \frac{\mathrm{d}\mathbf{x}}{\mathrm{d}t}$. This suggests the following numerical approximation: Assume we know the state of the system at a (discrete) time point $n$, denoted $x_n$, and that the change in the system is constant over a small interval $\Delta_t$. Then, the position of the system at time point $n + 1$ is given by:
\[\mathbf{x}_{n + 1} = \mathbf{x}_n + \Delta t \cdot f(\mathbf{x}_n) \enspace .\]$\Delta t$ is an important parameter, encoding over what time period we assume the change $f$ to be constant. We can code this up in R for the logistic equation:
solve_logistic <- function(N0, r = 1, delta_t = 0.01, times = 1000) {
N <- rep(N0, times)
dN <- function(N) r * N * (1 - N)
for (i in seq(2, times)) {
# Euler
N[i] <- N[i-1] + delta_t * dN(N[i-1])
# Improved Euler
# k <- N[i-1] + delta_t * dN(N[i-1])
# N[i] <- N[i-1] + 1 /2 * delta_t * (dN(N[i-1]) + dN(k))
# Runge-Kutta 4th order
# k1 <- dN(N[i-1]) * delta_t
# k2 <- dN(N[i-1] + k1/2) * delta_t
# k3 <- dN(N[i-1] + k2/2) * delta_t
# k4 <- dN(N[i-1] + k3) * delta_t
#
# N[i] <- N[i-1] + 1/6 * (k1 + 2*k2 + 2*k3 + k4)
}
N
}Clearly, the accuracy of this approximation is a function of $\Delta t$. To see how, the left panel shows the approximation for various values of $\Delta t$, while the right panel shows the (log) absolute error as a function of (log) $\Delta t$. The error is defined as:
\[E = |N(10) - \hat{N}(10)| \enspace ,\]where $\hat{N}$ is the Euler approximation.
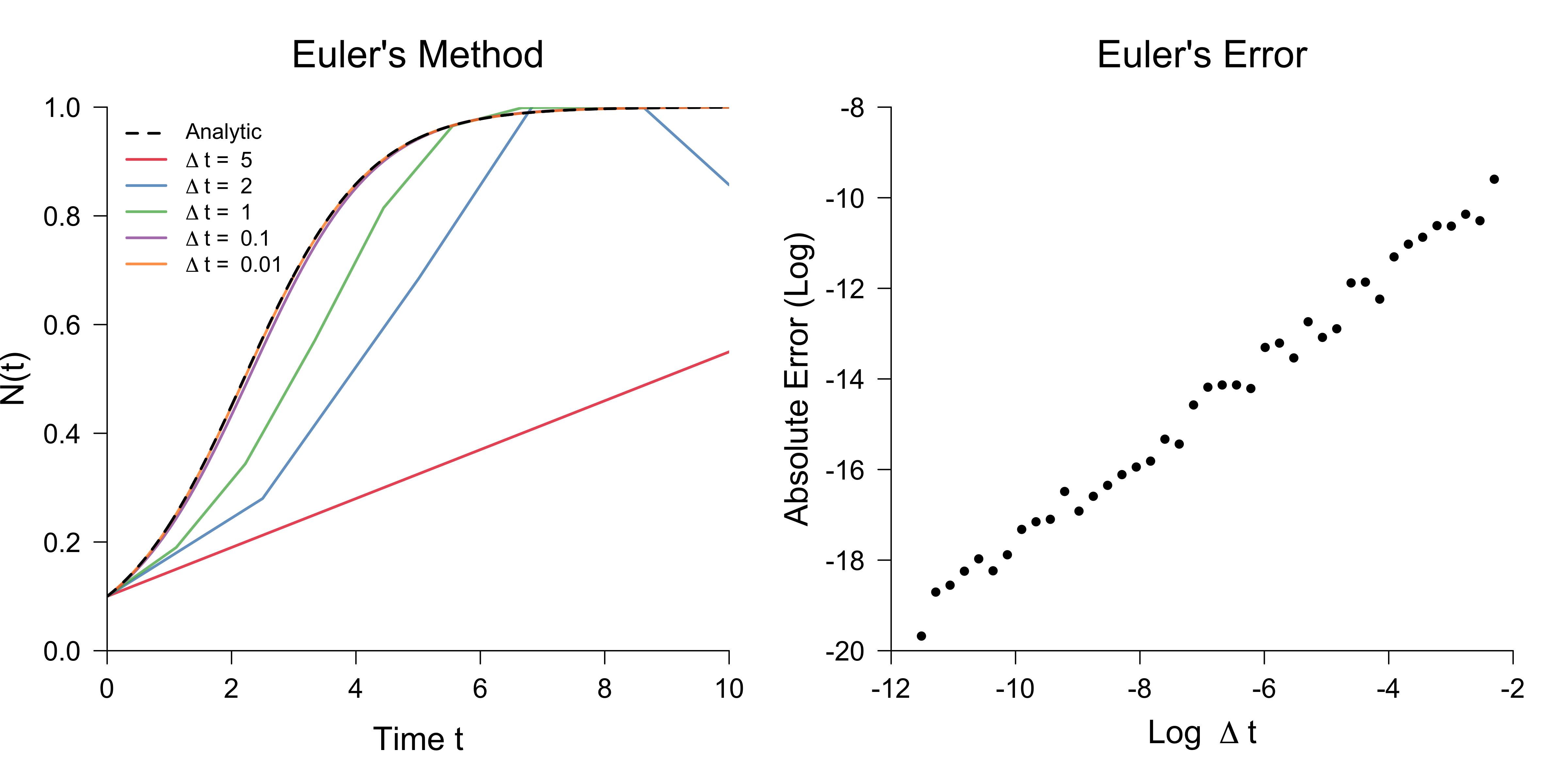
The right panel approximately shows the relationship:
\[\begin{aligned} \text{log } E &\propto \text{log } \Delta t \\[0.50em] E &\propto \Delta t \enspace . \end{aligned}\]Therefore, the error goes down linearly with $\Delta t$. Other methods, such as the improved Euler method or Runge-Kutta solvers (see commented out code above) do better. However, it is ill-advised to choose $\Delta t$ extremely small, because this leads to an increase in computation time and can lead to accuracy errors which get exacerbated over time.
In summary, we have seen that nonlinear differential equations can model interesting behaviour such as multiple fixed points; how to classify the stability of these fixed points using linear stability analysis; and how to numerically solve nonlinear differential equations. In the remainder of this post, we study coupled nonlinear differential equations — the SIR and SIRS models — as a way to model the spread of infectious diseases.
Modeling Infectious Diseases
Many models have been proposed as tools to understand epidemics. In the following sections, I focus on the two simplest ones: the SIR and the SIRS model (see also Hirsch, Smale, Devaney, 2013, ch. 11).
The SIR Model
We use the SIR model to understand the spread of infectious diseases. The SIR model is the most basic compartmental model, meaning that it groups the overall population into distinct sub-populations: a susceptible population $S$, an infected population $I$, and a recovered population $R$. We make a number of further simplifying assumptions. First, we assume that the overall population is $1 = S + I + R$ so that $S$, $I$, and $R$ are proportions. We further assume that the overall population does not change, that is,
\[\frac{d}{dt} \left(S + I + R\right) = 0 \enspace .\]Second, the SIR model assumes that once a person has been infected and has recovered, the person cannot become infected again — we will relax this assumption later on. Third, the model assumes that the rate of transmission of the disease is proportional to the number of encounters between susceptible and infected persons. We model this by setting
\[\frac{dS}{dt} = - \beta IS \enspace ,\]where $\beta > 0$ is the rate of infection. Fourth, the model assumes that the growth of the recovered population is proportional to the proportion of people that are infected, that is,
\[\frac{dR}{dt} = \gamma I \enspace ,\]where the $\gamma > 0$ is the recovery rate. Since the overall population is constant, these two equations naturally lead to the following equation for the infected:
\[\begin{aligned} \frac{d}{dt} \left(S + I + R\right) = 0 \\[0.50em] \frac{dI}{dt} = - \frac{dS}{dt} - \frac{dR}{dt} \\[0.50em] \frac{dI}{dt} = \beta IS - \gamma I \enspace . \end{aligned}\]where $\beta I S$ gives the proportion of newly infected individuals and $\gamma I$ gives the proportion of newly recovered individuals. Observe that since we assumed that the overall population does not change, we only need to focus on two of these subgroup, since $R(t) = 1 - S(t) - I(t)$. The system is therefore fully characterized by
\[\begin{aligned} \frac{dS}{dt} &= - \beta IS \\[0.50em] \frac{dI}{dt} &= \beta IS - \gamma I \enspace . \end{aligned}\]Before we analyze this model mathematically, let’s implement Euler’s method and visualize some trajectories.
solve_SIR <- function(S0, I0, beta = 1, gamma = 1, delta_t = 0.01, times = 8000) {
res <- matrix(
NA, nrow = times, ncol = 4, dimnames = list(NULL, c('S', 'I', 'R', 'Time'))
)
res[1, ] <- c(S0, I0, 1 - S0 - I0, delta_t)
dS <- function(S, I) -beta * I * S
dI <- function(S, I) beta * I * S - gamma * I
for (i in seq(2, times)) {
S <- res[i-1, 1]
I <- res[i-1, 2]
res[i, 1] <- res[i-1, 1] + delta_t * dS(S, I)
res[i, 2] <- res[i-1, 2] + delta_t * dI(S, I)
res[i, 4] <- delta_t * i
}
res[, 3] <- 1 - res[, 1] - res[, 2]
res
}
plot_SIR <- function(res, main = '') {
cols <- brewer.pal(3, 'Set1')
time <- res[, 4]
matplot(
time, res[, 1:3], type = 'l', col = cols, axes = FALSE, lty = 1, lwd = 2,
ylab = 'Subpopulations', xlab = 'Days', xlim = c(0, tail(time, 1)),
ylim = c(0, 1), main = main, cex.main = 1.75, cex.lab = 1.5,
xaxs = 'i', yaxs = 'i'
)
axis(1, cex.axis = 1.25)
axis(2, las = 2, cex.axis = 1.25)
legend(
30, 0.65, col = cols, legend = c('S', 'I', 'R'),
lty = 1, lwd = 2, bty = 'n', cex = 1.5
)
}The figure below shows trajectories for a fixed recovery rate of $\gamma = 1/8$ and an increasing rate of infection $\beta$ for the initial condition $S_0 = 0.95$, $I_0 = 0.05$, and $R_0 = 0$. We take a time step $\Delta t = 1$ to denote one day. (Unfortunately, epidemics take much longer in real life.)
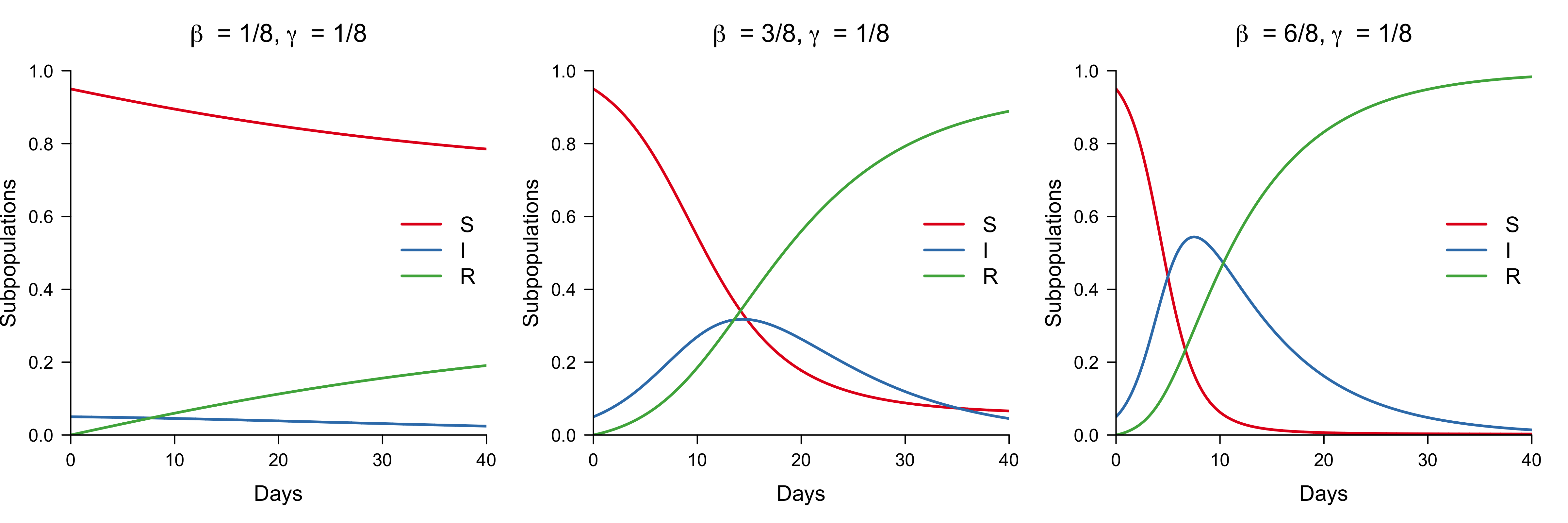
For $\beta = 1/8$, no outbreak occurs (left panel). Instead, the proportion of susceptible and infected people monotonically decrease while the proportion of recovered people monotonically increases. The middle panel, on the other hand, shows a small outbreak. The proportion of infected people rises, but then falls again. Similarly, the right panel shows an outbreak as well, but a more severe one, as the proportion of infected people rises more starkly before it eventually decreases again.
How do things change when we change the recovery rate $\gamma$? The figure below shows again three cases of trajectories for the same initial condition, but for a smaller recovery rate $\gamma = 1/12$.
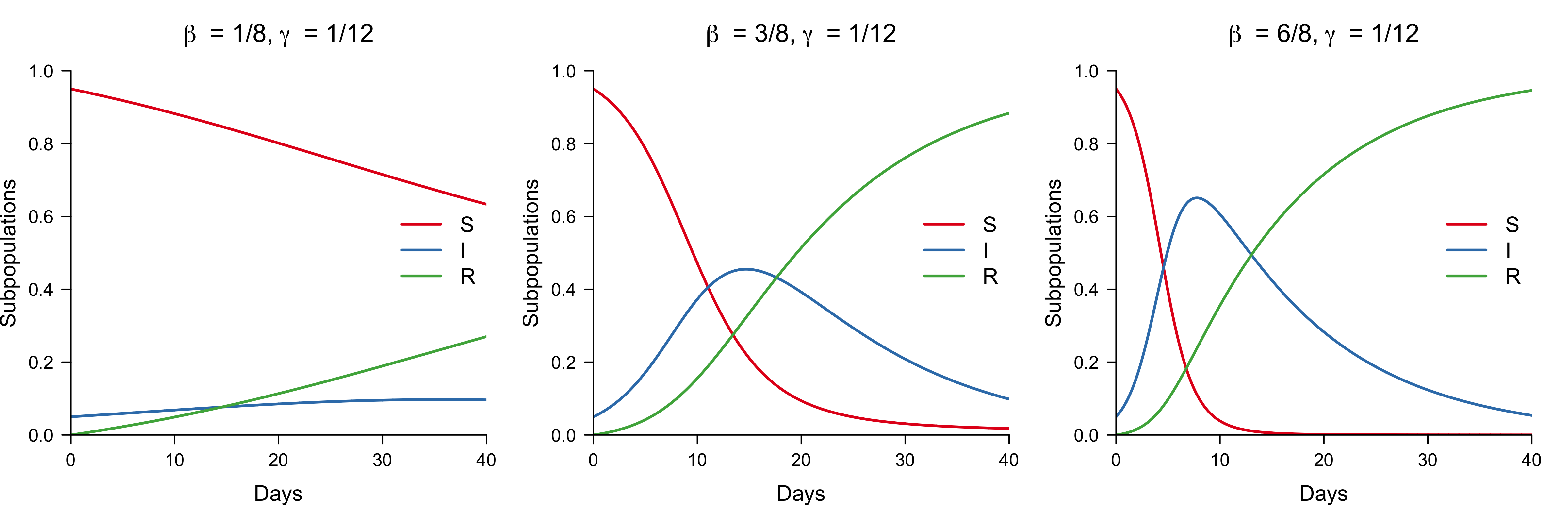
We again observe no outbreak in the left panel, and outbreaks of increasing severity in both the middle and the right panel. In contrast to the results for $\gamma = 1/8$, the outbreak is more severe, as we would expect since the recovery rate with $\gamma = 1/12$ is now lower. In fact, whether an outbreak occurs or not and how severe it will be depends not on $\beta$ and $\gamma$ alone, but on their ratio. This ratio is known as $R_0 = \beta / \gamma$, pronounced “R-naught”. (Note the unfortunate choice of well-established terminology in this context, as $R_0$ also denotes the initial proportion of recovered people; it should be clear from the context which one is meant, however.) We can think of $R_0$ as the average number of people an infected person will infect before she gets better (assuming a population that is fully susceptible). If $R_0 > 1$, an outbreak occurs. In the next section, we look for the fixed points of this system and assess their stability.
Analyzing Fixed Points
A glance at the above figures suggests that the SIR model allows for multiple stable states. The left panels, for example, show that if there is no outbreak, the proportion of susceptible people stays above the proportion of recovered people. If there is an outbreak, however, then it always fades and the proportion of recovered people will be higher than the proportion of susceptible people; how much higher depends on the severity of the outbreak.
While we could play around some more with visualisations, it pays to do a formal analysis. Note that in contrast to the logistic equation, which only modelled a single variable — population size — an analysis of the SIR model requires us to handle two variables, $S$ and $I$; the third one, $R$, follows from the assumption of a constant population size. At the fixed points, nothing changes, that is, we have:
\[\begin{aligned} 0 &= - \beta IS \\[0.50em] 0 &= \beta IS - \gamma I \enspace . \end{aligned}\]This can only happen when $I = 0$, irrespective of the value of $S$. In other words, all $(I^{\star}, S^{\star}) = (0, S)$ are fixed points; if nobody is infected, the disease cannot spread — and so everybody stays either susceptible or recovered. To assess the stability of these fixed points, we again derive a differential equation for the perturbations close to the fixed point. However, note that in contrast to the one-dimensional case studied above, perturbations can now be with respect to $I$ or to $S$. Let $u = S - S^{\star}$ and $v = I - I^{\star}$ be the respective perturbations, and let $\dot{S} = f(S, I)$ and $\dot{I} = g(S, I)$. We first derive a differential equation for $u$, writing:
\[\dot{u} = \frac{d}{dt}\left(S - S^{\star}\right) = \dot{S} \enspace ,\]since $S^{\star}$ is a constant. This implies that $u$ behaves as $S$. In contrast to the one-dimensional case above, we have two coupled differential equations, and so we have to take into account how $u$ changes as a function of both $S$ and $I$. We Taylor expand at the fixed point $(S^{\star}, I^{\star})$:
\[\begin{aligned} \dot{u} &= f(u + S^{\star}, v + I^{\star}) \\[0.50em] &= f(S^{\star}, I^{\star}) + u \frac{\partial f}{\partial S}_{(S^{\star}, I^{\star})} + v \frac{\partial f}{\partial I}_{(S^{\star}, I^{\star})} + \mathcal{O}(u^2, v^2, uv) \\[0.50em] &\approx u \frac{\partial f}{\partial S}_{(S^{\star}, I^{\star})} + v \frac{\partial f}{\partial I}_{(S^{\star}, I^{\star})} \enspace , \end{aligned}\]since $f(S^{\star}, I^{\star}) = 0$ and we drop higher-order terms. Note that taking the partial derivative of $f$ with respect to $S$ (or $I$) yields a function, and the subscripts $(S^{\star}, I^{\star})$ mean that we evaluate this function at the fixed point $(S^{\star}, I^{\star})$. We can similarly derive a differential equation for $v$:
\[\dot{v} \approx u \frac{\partial g}{\partial S}_{(S^{\star}, I^{\star})} + v \frac{\partial g}{\partial I}_{(S^{\star}, I^{\star})} \enspace .\]We can write all of this concisely using matrix algebra:
\[\begin{pmatrix} \dot{u} \\ \dot{v} \end{pmatrix} = \begin{pmatrix} \frac{\partial f}{\partial S} & \frac{\partial f}{\partial I} \\ \frac{\partial g}{\partial S} & \frac{\partial g}{\partial I} \end{pmatrix}_{(S^{\star}, I^{\star})} \begin{pmatrix} u \\ v \end{pmatrix} \enspace ,\]where
\[J = \begin{pmatrix} \frac{\partial f}{\partial S} & \frac{\partial f}{\partial I} \\ \frac{\partial g}{\partial S} & \frac{\partial g}{\partial I} \end{pmatrix}_{(S^{\star}, I^{\star})}\]is called the Jacobian matrix at the fixed point $(S^{\star}, I^{\star})$. The Jacobian gives the linearized dynamics close to a fixed point, and therefore tells us how perturbations will evolve close to a fixed point.
In contrast to unidimensional systems, where we simply check whether the slope is positive or negative, that is, whether $f’(x^\star) < 0$ or $f’(x^\star) > 0$, the test for whether a fixed point is stable is slightly more complicated in multidimensional settings. In fact, and not surprisingly, since we have linearized this nonlinear differential equation, the check is the same as in linear systems: we compute the eigenvalues $\lambda_1$ and $\lambda_2$ of $J$, observing that negative eigenvalues mean exponential decay and positive eigenvalues mean exponential growth along the directions of the respective eigenvectors. (Note that this does not work for all types of fixed points, see Strogatz (2015, p. 152).)
What does this mean for our SIR model? First, let’s derive the Jacobian:
\[\begin{aligned} J &= \begin{pmatrix} -\frac{\partial}{\partial S} \beta I S & -\frac{\partial }{\partial I} \beta I S \\ \frac{\partial}{\partial S} \left(\beta I S - \gamma I\right) & \frac{\partial}{\partial I} \left(\beta I S - \gamma I\right) \\[0.5em] \end{pmatrix} \\[1em] & = \begin{pmatrix} -\beta I & -\beta S \\ \beta I & \beta S - \gamma \end{pmatrix} \enspace . \end{aligned}\]Evaluating this at the fixed point $(S^{\star}, I^{\star}) = (S, 0)$ results in:
\[J_{(S, 0)} = \begin{pmatrix} 0 & -\beta S \\ 0 & \beta S - \gamma \end{pmatrix} \enspace .\]Since this matrix is upper triangular — all entries below the diagonal are zero — the eigenvalues are given by the diagonal, that is, $\lambda_1 = 0$ and $\lambda_2 = \beta S - \gamma$. $\lambda_1 = 0$ implies a constant solution, while $\lambda_2 > 0$ implies exponential growth and $\lambda_2 < 0$ exponential decay of the perturbations close to the fixed point. Observe that $\lambda_2$ is not only a function of the parameters $\beta$ and $\gamma$, but also of the proportion of susceptible individuals $S$. We find that $\lambda_2 > 0$ for $S > \gamma / \beta$, which results in an unstable fixed point. On the other hand, we have that $\lambda_2 < 0$ for $S < \gamma / \beta$, which results in a stable fixed point. In the next section, we will use vector fields in order to get more intuition for the dynamics of the system.
Vector Field and Nullclines
A vector field shows for any position $(S, I)$ in which direction the system moves, which we indicate by the head of an arrow, and how quickly, which we indicate by the length of an arrow. We use the R code below to visualize such a vector field and selected trajectories on it.
library('fields')
plot_vectorfield_SIR <- function(beta, gamma, main = '', ...) {
S <- seq(0, 1, 0.05)
I <- seq(0, 1, 0.05)
dS <- function(S, I) -beta * I * S
dI <- function(S, I) beta * I * S - gamma * I
SI <- as.matrix(expand.grid(S, I))
SI <- SI[apply(SI, 1, function(x) sum(x) <= 1), ] # S + I <= 1 must hold
dSI <- cbind(dS(SI[, 1], SI[, 2]), dI(SI[, 1], SI[, 2]))
draw_vectorfield(SI, dSI, main, ...)
}
draw_vectorfield <- function(SI, dSI, main, ...) {
S <- seq(0, 1, 0.05)
I <- seq(0, 1, 0.05)
plot(
S, I, type = 'n', axes = FALSE, xlab = '', ylab = '', main = '',
cex.main = 1.5, xlim = c(-0.2, 1), ylim = c(-0.2, 1.2), ...
)
lines(c(-0.1, 1), c(0, 0), lwd = 1)
lines(c(0, 0), c(-0.1, 1), lwd = 1)
arrow.plot(
SI, dSI,
arrow.ex = .075, length = .05, lwd = 1.5, col = 'gray82', xpd = TRUE
)
cx <- 1.5
cn <- 2
text(0.5, 1.05, main, cex = 1.5)
text(0.5, -.075, 'S', cex = cn, font = 1)
text(-.05, 0.5, 'I', cex = cn, font = 1)
text(-.03, -.04, 0, cex = cx, font = 1)
text(-.03, .975, 1, cex = cx, font = 1)
text(0.995, -0.04, 1, cex = cx, font = 1)
}For $\beta = 1/8$ and $\gamma = 1/8$, we know from above that no outbreak occurs. The vector field shown in the left panel below further illustrates that, since $S \leq \gamma / \beta = 1$, all fixed points $(S^{\star}, I^{\star}) = (S, 0)$ are stable. In contrast, we know that $\beta = 3/8$ and $\gamma = 1/8$ result in an outbreak. The vector field shown in the right panel below indicates that fixed points with $S > \gamma / \beta = 1/3$ are unstable, while fixed points with $S < 1/3$ are stable; the dotted line is $S = 1/3$.
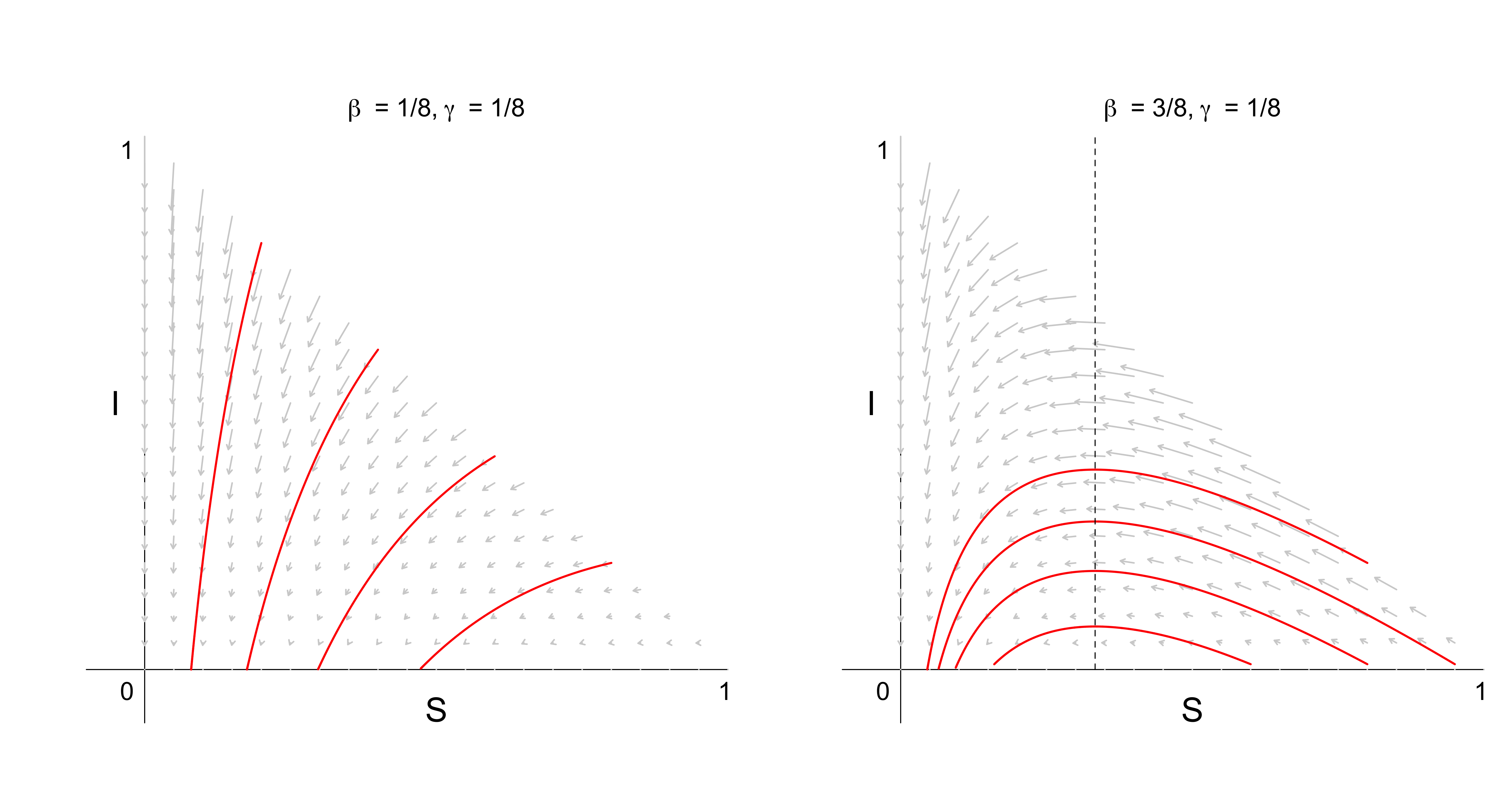
Can we find some structure in such vector fields? One way to “organize” them is by drawing so-called nullclines. In our case, the $I$-nullcline gives the set of points for which $\dot{I} = 0$, and the $S$-nullcline gives the set of points for which $\dot{S} = 0$. We find these points in a similar manner to finding fixed points, but instead of setting both $\dot{S}$ and $\dot{I}$ to zero, we tackle them one at a time.
The $S$-nullclines are given by the $S$- and the $I$-axes, because $\dot{S} = 0$ when $S = 0$ or when $I = 0$. Along the $I$-axis axis we have $\dot{I} = - \gamma I$ since $S = 0$, resulting in exponential decay of the infected population; this indicated by the grey arrows along the $I$-axis which are of progressively smaller length the closer they approach the origin.
The $I$-nullclines are given by $I = 0$ and by $S = \gamma / \beta$. For $I = 0$, we have $\dot{S} = 0$ and so these yield fixed points. For $S = \gamma / \beta$ we have $\dot{S} = - \gamma I$, resulting in exponential decay of the susceptible population, but since $\dot{I} = 0$, the proportion of infected people does not change; this is indicated in the left vector field above, where we have horizontal arrows at the dashed line given by $S = \gamma / \beta$. However, this only holds for the briefest of moments, since $S$ decreases and for $S < \gamma / \beta$ we again have $\dot{I} < 0$, and so the proportion of infected people goes down to the left of the line. Similarly, to the right of the line we have $S > \gamma / \beta$, which results in $\dot{I} > 0$, and so the proportion of infected people grows.
In summary, we have seen how the SIR model allows for outbreaks whenever the rate of infection is higher than the rate of recovery, $R_0 > \beta / \gamma$. If this occurs, then we have a growing proportion of infected people while $S > \gamma / \beta$. As illustratd by the vector field, the proportion of susceptible people $S$ decreases over time. At some point, therefore, we have that $S < \gamma / \beta$, resulting in a decrease in the proportion of infected people until finally $I = 0$. Observe that, in the SIR model, infections always die out. In the next section, we extend the SIR model to allow for diseases to become established in the population.
The SIRS Model
The SIR model assumes that once infected people are immune to the disease forever, and so any disease occurs only once and then never comes back. More interesting dynamics occur when we allow for the reinfection of recovered people; we can then ask, for example, under what circumstances the disease becomes established in the population. The SIRS model extends the SIR model, allowing the recovered population to become susceptible again (hence the extra ‘S’). It assumes that the susceptible population increases proportional to the recovered population such that:
\[\begin{aligned} \frac{dS}{dt} &= - \beta IS + \mu R \\[0.50em] \frac{dI}{dt} &= \beta IS - \gamma I \\[0.50em] \frac{dR}{dt} &= \gamma I - \mu R\enspace , \end{aligned}\]where, since we added $\mu R$ to the change in the proportion of susceptible people, we had to subtract $\mu R$ from the change in the proportion of recovered people. We again make the simplifying assumption that the overall population does not change, and so it suffices to study the following system:
\[\begin{aligned} \frac{dS}{dt} &= - \beta IS + \mu R \\[0.50em] \frac{dI}{dt} &= \beta IS - \gamma I \enspace , \end{aligned}\]since $R(t) = 1 - S(t) - I(t)$. We adjust our implementation of Euler’s method:
solve_SIRS <- function(
S0, I0, beta = 1, gamma = 1, mu = 1, delta_t = 0.01, times = 1000
) {
res <- matrix(
NA, nrow = times, ncol = 4, dimnames = list(NULL, c('S', 'I', 'R', 'Time'))
)
res[1, ] <- c(S0, I0, 1 - S0 - I0, delta_t)
dS <- function(S, I, R) -beta * I * S + mu * R
dI <- function(S, I, R) beta * I * S - gamma * I
for (i in seq(2, times)) {
S <- res[i-1, 1]
I <- res[i-1, 2]
R <- res[i-1, 3]
res[i, 1] <- res[i-1, 1] + delta_t * dS(S, I, R)
res[i, 2] <- res[i-1, 2] + delta_t * dI(S, I, R)
res[i, 3] <- 1 - res[i, 1] - res[i, 2]
res[i, 4] <- i * delta_t
}
res
}
plot_SIRS <- function(res, main = '') {
cols <- brewer.pal(3, 'Set1')
time <- res[, 4]
matplot(
time, res[, 1:3], type = 'l', col = cols, axes = FALSE, lty = 1, lwd = 2,
ylab = 'Subpopulations', xlab = 'Days', ylim = c(0, 1),
main = main, cex.main = 1.75, cex.lab = 1.25,
font.main = 1, xaxs = 'i', yaxs = 'i', xlim = c(0, tail(time, 1))
)
axis(1, cex.axis = 1.5)
axis(2, las = 2, cex.axis = 1.5)
legend(
30, 0.95, col = cols, legend = c('S', 'I', 'R'),
lty = 1, lwd = 2, bty = 'n', cex = 1.5
)
}The figure below shows trajectories for a fixed recovery rate of $\gamma = 1/8$, a fixed reinfection rate of $\mu = 1/8$, and an increasing rate of infection $\beta$ for the initial condition $S_0 = 0.95$, $I_0 = 0.05$, and $R_0 = 0$.
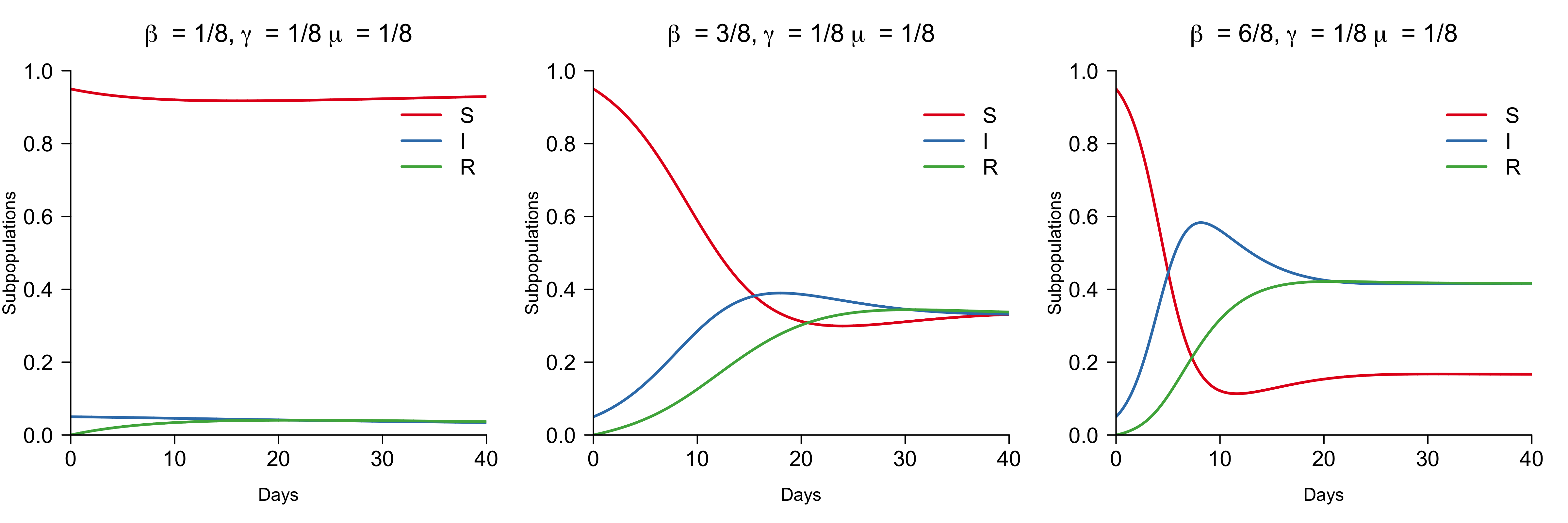
As for the SIR model, we again find that no outbreak occurs for $R_0 = \beta / \gamma < 1$, which is the case for the left panel. Most interestingly, however, we find that the proportion of infected people does not, in contrast to the SIR model, decrease to zero for the other panels. Instead, the disease becomes established in the population when $R_0 > 1$, and the middle and the right panel show different fixed points.
How do things change when we vary the reinfection rate $\mu$? The figure below shows again three cases of trajectories for the same initial condition, but for a smaller reinfection rate $\mu$.
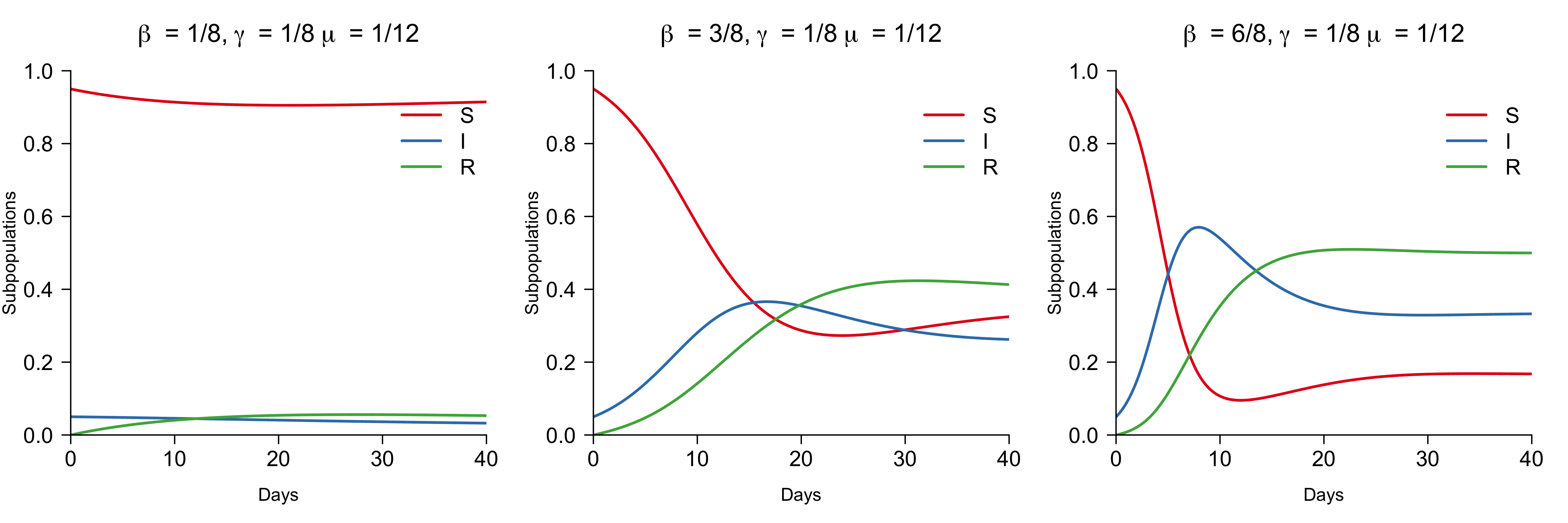
We again find no outbreak in the left panel, and outbreaks of increasing severity in the middle and right panel. Both these outbreaks are less severe compared to the outbreaks in the previous figures, as we would expect given a decrease in the reinfection rate. Similarly, the system seems to stabilize at different fixed points. In the next section, we provide a more formal analysis of the fixed points and their stability.
Analyzing Fixed Points
To find the fixed points of the SIRS model, we again seek solutions for which:
\[\begin{aligned} 0 &= - \beta IS + \mu (1 - S - I) \\[0.50em] 0 &= \beta IS - \gamma I \enspace , \end{aligned}\]where we have substituted $R = 1 - S - I$ and from which it follows that also $\dot{R} = 0$ since we assume that the overall population does not change. We immediately see that, in contrast to the SIR model, $I = 0$ cannot be a fixed point for any $S$ because of the added term which depends on $\mu$. Instead, it is a fixed point only for $S = 1$. To get the other fixed point, note that the last equation gives $S = \gamma / \beta$, which plugged into the first equation yields:
\[\begin{aligned} 0 &= -I\gamma + \mu\left(1 - \frac{\gamma}{\beta} - I\right) \\[0.50em] I\gamma &= \mu\left(1 - \frac{\gamma}{\beta}\right) - \mu I \\[0.50em] I(\gamma + \mu) &= \mu\left(1 - \frac{\gamma}{\beta}\right) \\[0.50em] I &= \frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu} \enspace . \end{aligned}\]Therefore, the fixed points are:
\[\begin{aligned} (S^{\star}, I^{\star}) &= (1, 0) \\[0.50em] (S^{\star}, I^{\star}) &= \left(\frac{\gamma}{\beta}, \frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu}\right) \enspace . \end{aligned}\]Note that the second fixed point does not exist when $\gamma / \beta > 1$, since the proportion of infected people cannot be negative. Another, more intuitive perspective on this is to write $\gamma / \beta > 1$ as $R_0 = \beta / \gamma < 1$. This allows us to see that the second fixed point, which would have a non-zero proportion of infected people in the population, does not exist when $R_0 < 1$, as then no outbreak occurs. We will come back to this in a moment.
To assess the stability of the fixed points, we derive the Jacobian matrix for the SIRS model:
\[\begin{aligned} J &= \begin{pmatrix} \frac{\partial}{\partial S} \left(-\beta I S + \mu(1 - S - I)\right) & \frac{\partial }{\partial I} \left(-\beta I S + \mu(1 - S - I)\right) \\ \frac{\partial}{\partial S} \left(\beta I S - \gamma I\right) & \frac{\partial}{\partial I} \left(\beta I S - \gamma I\right) \\[0.5em] \end{pmatrix} \\[1em] &= \begin{pmatrix} -\beta I - \mu & -\beta S - \mu \\ \beta I & \beta S - \gamma \end{pmatrix} \enspace . \end{aligned}\]For the fixed point $(S^{\star}, I^{\star}) = (1, 0)$ we have:
\[J_{(1, 0)} = \begin{pmatrix} - \mu & -\beta - \mu \\ 0 & \beta - \gamma \end{pmatrix} \enspace ,\]which is again upper-triangular and therefore has eigenvalues $\lambda_1 = -\mu$ and $\lambda_2 = \beta - \gamma$. This means it is unstable whenever $\beta > \gamma$ since then $\lambda_2 > 0$, and any infected individual spreads the disease. The Jacobian at the second fixed point is:
\[J_{\left(\frac{\gamma}{\beta}, \frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu}\right)} = \begin{pmatrix} -\beta\frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu} - \mu & -\gamma - \mu \\ \beta\frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu} & - 2\gamma \end{pmatrix} \enspace ,\]which is more daunting. However, we know from the previous blog post that to classify the stability of the fixed point, it suffices to look at the trace $\tau$ and determinant $\Delta$ of the Jacobian, which are given by
\[\begin{aligned} \tau &= -\beta\frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu} - 2\gamma \\[0.50em] \Delta &= \left(-\beta\frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu}\right)\left(-2\gamma\right) - \left(- \gamma - \mu\right)\left(\beta\frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu}\right) \\[0.50em] &= 2\gamma\beta\frac{\mu\left(1 - \frac{\gamma}{\beta}\right)}{\gamma + \mu} + \beta\mu\left(1 - \frac{\gamma}{\beta}\right) \enspace . \end{aligned}\]The trace can be written as $\tau = \lambda_1 + \lambda_2$ and the determinant can be written as $\Delta = \lambda_1 \lambda_2$, as shown in a previous blog post. Here, we have that $\tau < 0$ because both terms above are negative, and $\Delta > 0$ because both terms above are positive. This constrains $\lambda_1$ and $\lambda_2$ to be negative, and thus the fixed point is stable.
Vector Fields and Nullclines
As previously done for the SIR model, we can again visualize the directions in which the system changes at any point using a vector field.
plot_vectorfield_SIRS <- function(beta, gamma, mu, main = '', ...) {
S <- seq(0, 1, 0.05)
I <- seq(0, 1, 0.05)
dS <- function(S, I) -beta * I * S + mu * (1 - S - I)
dI <- function(S, I) beta * I * S - gamma * I
SI <- as.matrix(expand.grid(S, I))
SI <- SI[apply(SI, 1, function(x) sum(x) <= 1), ] # S + I <= 1 must hold
dSI <- cbind(dS(SI[, 1], SI[, 2]), dI(SI[, 1], SI[, 2]))
draw_vectorfield(SI, dSI, main, ...)
}The figure below visualizes the vector field for the SIRS model, several trajectories, and the nullclines for $\gamma = 1/8$ and $\mu = 1/8$ for $\beta = 1/8$ (left panel) and $\beta = 3/8$ (right panel). The left panel shows that there exists only one stable fixed point at $(S^{\star}, I^{\star}) = (1, 0)$ to which all trajectories converge.
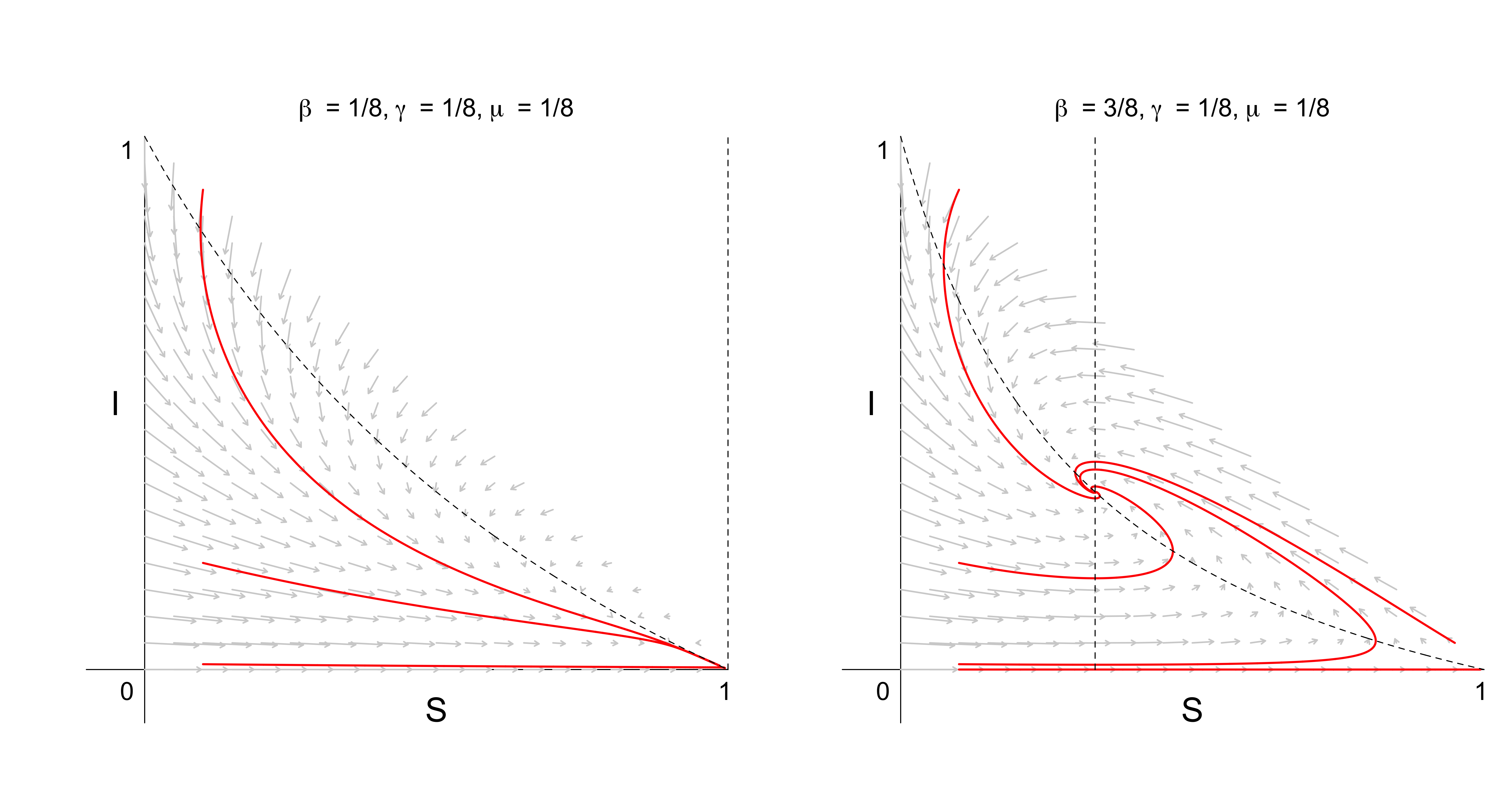
The right panel, on the other hand, shows two fixed points: one unstable fixed point at $(S^{\star}, I^{\star}) = (1, 0)$, which we only reach when $I_0 = 0$, and a stable one at
\[(S^{\star}, I^{\star}) = \left(\frac{1/8}{3/8}, \frac{1/8\left(1 - \frac{3/8}{1/8}\right)}{1/8 + 1/8}\right) = (1/3, 1/3) \enspace .\]In contrast to the SIR model, therefore, there exists a stable fixed point constituting a population which includes infected people, and so the disease is not eradicated but stays in the population.
The dashed lines give the nullclines. The $I$-nullcline gives the set of points where $\dot{I} = 0$, which are — as in the SIR model above — given by $I = 0$ and $S = \gamma / \beta$. The $S$-nullcline is given by:
\[\begin{aligned} 0 &= - \beta I S + \mu(1 - S - I) \\[0.50em] \beta I S &= \mu(1 - S) - \mu I \\[0.50em] I &= \frac{\mu(1 - S)}{\beta S + \mu} \enspace , \end{aligned}\]which is a nonlinear function in $S$. The nullclines help us again in “organizing” the vector field. This can be seen best in the right panel above. In particular, and similar to the SIR model, we will again have a decrease in the proportion of infected people to the left of the line given by $S = \gamma / \beta$, that is, when $S < \gamma / \beta$, and an increase to the right of the line, that is, when $S > \gamma / \beta$. Similarly, the proportion of susceptible people increases when the system is “below” the $S$-nullcline, while it increases when the system is “above” the $S$-nullcline.
Bifurcations
In the vector fields above we have seen that the system can go from having only one fixed point to having two fixed points. Whenever a fixed point is destroyed or created or changes its stability as an internal parameter is varied — here the ratio of $\gamma / \beta$ — we speak of a bifurcation.
As pointed out above, the second equilibrium point only exists for $\gamma / \beta \leq 1$. As long as $\gamma / \beta < 1$, we have two distinct fixed points. At $\gamma / \beta = 1$, the second fixed point becomes:
\[\begin{aligned} (S^{\star}, I^{\star}) &= \left(1, \frac{\mu\left(1 - 1\right)}{\gamma + \mu}\right) = (1, 0) \enspace , \end{aligned}\]which equals the first fixed point. Thus, at $\gamma / \beta = 1$, the two fixed points merge into one; this is the bifurcation point. This makes sense: if $\gamma / \beta < 1$, we have that $\beta / \gamma > 1$, and so an outbreak occurs, which establishes the disease in the population since we allow for reinfections.
We can visualize this change in fixed points in a so-called bifurcation diagram. A bifurcation diagram shows how the fixed points and their stability change as we vary an internal parameter. Since we deal with two-dimensional fixed points, we split the bifurcation diagram into two: the left panel shows how the $I^{\star}$ part of the fixed point changes as we vary $\gamma / \beta$, and the right panel shows how the $S^{\star}$ part of the fixed point changes as we vary $\gamma / \beta$.
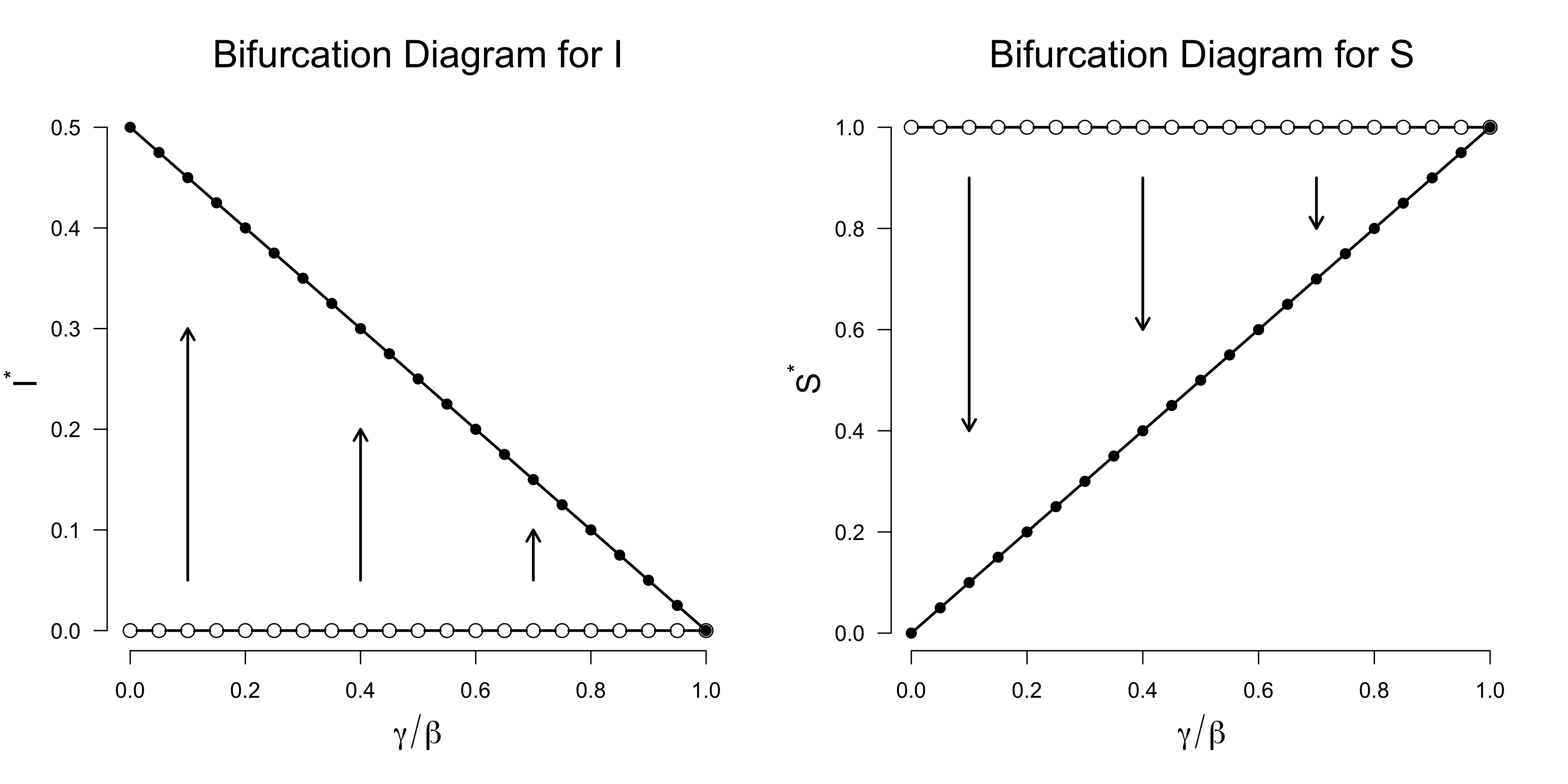
The left panel shows that as long as $\gamma / \beta < 1$, which implies that $\beta / \gamma > 1$, we have two fixed points where the stable fixed point is the one with a non-zero proportion of infected people — the disease becomes established. These fixed points are on the diagonal line, indicates as black dots. Interestingly, this shows that the proportion of infected people can never be stable at a value larger than $1/2$. There also exist unstable fixed points for which $I^{\star} = 0$. These fixed points are unstable because if there even exists only one infected person, she will spread the disease, resulting in more infected people. At the point where $\beta = \gamma$, the two fixed points merge: the disease can no longer be established in the population, and the proportion of infected people always goes to zero.
Similarly, the right panel shows how the fixed points $S^{\star}$ change as a function of $\gamma / \beta$. Since the infection spreads for $\beta > \gamma$, the fixed point $S^{\star} = 1$ is unstable, as the proportion of susceptible people must decrease since they become infected. For outbreaks that become increasingly mild as $\gamma / \beta \rightarrow 1$, the stable proportion of susceptible people increases, reaching $S^{\star} = 1$ when at last $\gamma = \beta$.
In summary, we have seen how the SIRS extends the SIR model by allowing reinfections. This resulted in possibility of more interesting fixed points, which included a non-zero proportion of infected people. In the SIRS model, then, a disease can become established in the population. In contrast to the SIR model, we have also seen that the SIRS model allows for bifuractions, going from two fixed points in times of outbreaks ($\beta > \gamma$) to one fixed point in times of no outbreaks ($\beta < \gamma$).
Conclusion
In this blog post, we have seen that nonlinear differential equations are a powerful tool to model real-world phenomena. They allow us to model vastly more complicated behaviour than is possible with linear differential equations, yet they rarely provide closed-form solution. Luckily, the time-evolution of a system can be straightforwardly computed with basic numerical techniques such as Euler’s method. Using the simple logistic equation, we have seen how to analyze the stability of fixed points — simply pretend the system is linear close to a fixed point.
The logistic equation has only one state variable — the size of the population. More interesting dynamics occur when variables interact, and we have seen how the simple SIR model can help us understand the spread of infectious disease. Consisting only of two parameters, we have seen that an outbreak occurs only when $R_0 = \beta / \gamma > 1$. Moreover, the stable fixed points always included $I = 0$, implying that the disease always gets eradicated. This is not true for all diseases because recovered people might become reinfected. The SIRS model amends this by introducing a parameter $\mu$ that quantifies how quickly recovered people can become susceptible again. As expected, this led to stable states in which the disease becomes established in the population.
On our journey to understand these systems, we have seen how to quantify the stability of a fixed point using linear stability analysis, how to visualize the dynamics of a system using vector fields, how nullclines give structure to such vector fields, and how bifurcations can drastically change the dynamics of a system.
The SIR and the SIRS models discussed here are without a doubt crude approximations of the real dynamics of the spread of infectious diseases. There exist several ways to extend them. One way to do so, for example, is to add an exposed population which are infected but are not yet infectious; see here for a visualization of an elaborated version of this model in the context of SARS-CoV-2. These basic compartment models assume homogeneity of spatial-structure, which is a substantial simplification. There are various ways to include spatial structure (e.g., Watts, 2005; Riley, 2007), but that is for another blog post.
I would like to thank Adam Finnemann, Anton Pichler, and Oísin Ryan for very helpful comments on this blog post.
References
- Strogatz, S. H. (2015). Nonlinear Dynamics and Chaos: With applications to Physics, Biology, Chemistry, and Engineering. Colorado, US: Westview Press.
- Hirsch, M. W., Smale, S., & Devaney, R. L. (2013). Differential equations, dynamical systems, and an introduction to chaos. Boston, US: Academic Press.
- Riley, S. (2007). Large-scale spatial-transmission models of infectious disease. Science, 316(5829), 1298-1301.
- Watts, D. J., Muhamad, R., Medina, D. C., & Dodds, P. S. (2005). Multiscale, resurgent epidemics in a hierarchical metapopulation model. Proceedings of the National Academy of Sciences, 102(32), 11157-11162.